Is 29 A Composite Or Prime Number
Arias News
Apr 01, 2025 · 5 min read
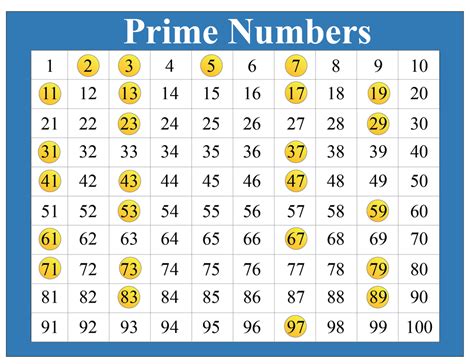
Table of Contents
Is 29 a Composite or Prime Number? A Deep Dive into Number Theory
Determining whether a number is prime or composite is a fundamental concept in number theory. This exploration will delve into the definition of prime and composite numbers, explain how to determine the primality of a number, and definitively answer the question: Is 29 a composite or prime number? We'll also touch upon the practical applications and significance of prime numbers in various fields.
Understanding Prime and Composite Numbers
Before we tackle the specific case of 29, let's establish a solid understanding of the core concepts.
Prime Numbers: The Building Blocks of Arithmetic
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. In simpler terms, it's only divisible by 1 and itself without leaving a remainder. The first few prime numbers are 2, 3, 5, 7, 11, 13, and so on. Prime numbers are the fundamental building blocks of all other whole numbers, a concept central to the Fundamental Theorem of Arithmetic, which states that every integer greater than 1 can be uniquely represented as a product of prime numbers.
Composite Numbers: The Products of Primes
A composite number, conversely, is a natural number greater than 1 that is not prime. This means it can be factored into smaller whole numbers other than 1 and itself. For instance, 6 is a composite number because it's divisible by 2 and 3 (6 = 2 x 3). Similarly, 12 is composite (12 = 2 x 2 x 3), as is 15 (15 = 3 x 5). Essentially, composite numbers are the result of multiplying two or more prime numbers (or other composite numbers).
The Number 1: Neither Prime Nor Composite
It's crucial to note that the number 1 is neither prime nor composite. It's a unique case excluded from both classifications. This distinction is essential for maintaining the integrity of the Fundamental Theorem of Arithmetic.
Determining Primality: Methods and Techniques
Several methods can determine whether a number is prime or composite. The complexity of these methods varies depending on the size of the number.
Trial Division: A Simple Approach for Smaller Numbers
For smaller numbers, trial division is a straightforward method. It involves systematically checking for divisibility by all prime numbers less than or equal to the square root of the number in question. If no such prime number divides the number evenly, it's considered prime.
Let's illustrate this with a simple example: To check if 13 is prime, we check its divisibility by prime numbers less than or equal to √13 (approximately 3.6). We test 2 and 3. Since 13 isn't divisible by 2 or 3, we conclude that 13 is prime.
However, for larger numbers, trial division becomes computationally expensive and inefficient.
More Advanced Techniques: For Larger Numbers
For significantly larger numbers, more sophisticated algorithms are necessary, such as the Sieve of Eratosthenes, the AKS primality test, and probabilistic tests like the Miller-Rabin primality test. These methods optimize the process of identifying prime numbers and are crucial in cryptography and other computationally intensive fields.
Is 29 a Composite or Prime Number? The Definitive Answer
Now, let's apply our knowledge to the number 29. Using trial division:
The square root of 29 is approximately 5.38. We need to check for divisibility by prime numbers less than or equal to 5, which are 2, 3, and 5.
- Divisibility by 2: 29 is not divisible by 2 (it's odd).
- Divisibility by 3: The sum of the digits of 29 (2 + 9 = 11) is not divisible by 3, so 29 is not divisible by 3.
- Divisibility by 5: 29 does not end in 0 or 5, so it's not divisible by 5.
Since 29 is not divisible by any prime number less than its square root, we can definitively conclude that 29 is a prime number.
The Significance of Prime Numbers
Prime numbers, seemingly abstract mathematical entities, hold immense practical significance in various fields:
Cryptography: Securing Digital Information
Prime numbers form the bedrock of many modern cryptographic systems. Algorithms like RSA encryption rely heavily on the difficulty of factoring large composite numbers into their prime factors. The security of online transactions, digital communication, and sensitive data protection depends on the properties of prime numbers.
Hashing and Data Structures: Efficient Data Management
Prime numbers are also used in hashing algorithms, which are crucial for efficient data storage and retrieval in computer science. Choosing prime numbers as the size of hash tables helps minimize collisions and ensures better performance.
Coding Theory: Error Detection and Correction
Prime numbers play a role in coding theory, used for error detection and correction in data transmission. These codes are critical in ensuring the reliability of data communication in various applications, from satellite communication to digital media.
Number Theory Research: An Ongoing Pursuit
Research in number theory continues to explore the fascinating properties of prime numbers. Questions like the distribution of prime numbers, the twin prime conjecture, and the Riemann hypothesis remain some of the most challenging unsolved problems in mathematics.
Conclusion: 29 – A Prime Example
In summary, we've explored the definitions of prime and composite numbers, discussed methods for determining primality, and decisively answered the question: 29 is a prime number. The seemingly simple concept of prime numbers has far-reaching implications across numerous fields, underscoring their importance in both theoretical mathematics and practical applications. Understanding prime numbers provides a foundation for appreciating the elegance and power of number theory and its role in shaping our technological world. Further exploration into the vast world of prime numbers will continue to unveil new insights and applications in the future.
Latest Posts
Latest Posts
-
How Tall Is 1 83 Meters In Feet
Apr 03, 2025
-
Ice Cream Flavors That Start With B
Apr 03, 2025
-
Lines That Intersect At A Right Angle
Apr 03, 2025
-
Will Wasp And Hornet Spray Kill Spiders
Apr 03, 2025
-
What Are The Common Multiples Of 5 And 10
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about Is 29 A Composite Or Prime Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
