Is 3 4 Bigger Than 5 8
Arias News
May 10, 2025 · 4 min read
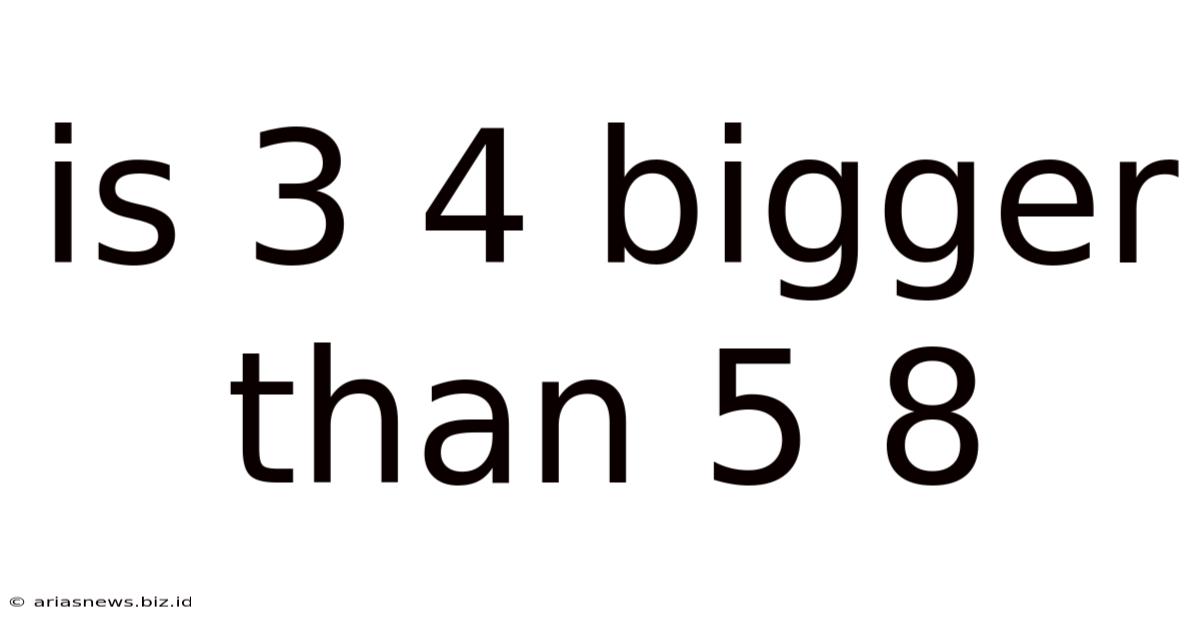
Table of Contents
Is 3/4 Bigger Than 5/8? A Deep Dive into Fraction Comparison
Determining whether 3/4 is bigger than 5/8 might seem like a simple task, especially for those comfortable with fractions. However, understanding the underlying principles behind fraction comparison is crucial for developing a strong foundation in mathematics. This article will not only answer the question definitively but will also explore various methods for comparing fractions, providing a comprehensive guide suitable for learners of all levels.
Understanding Fractions: A Quick Refresher
Before delving into the comparison, let's revisit the fundamental components of a fraction: the numerator and the denominator. The numerator represents the number of parts you have, while the denominator represents the total number of equal parts the whole is divided into. For instance, in the fraction 3/4, 3 is the numerator and 4 is the denominator. This means we have 3 out of 4 equal parts of a whole.
Method 1: Finding a Common Denominator
This is arguably the most common and reliable method for comparing fractions. The core idea is to convert both fractions into equivalent fractions that share the same denominator. This allows for a direct comparison of their numerators.
Steps:
-
Find the Least Common Multiple (LCM): Determine the least common multiple of the denominators (4 and 8 in this case). The LCM of 4 and 8 is 8.
-
Convert the Fractions:
- For 3/4, we multiply both the numerator and the denominator by 2 (because 8 / 4 = 2): (3 x 2) / (4 x 2) = 6/8
- 5/8 remains unchanged as it already has a denominator of 8.
-
Compare the Numerators: Now we compare 6/8 and 5/8. Since 6 > 5, we conclude that 6/8 > 5/8, and therefore, 3/4 > 5/8.
Method 2: Converting to Decimals
Another effective method involves converting the fractions into their decimal equivalents. This approach is particularly helpful when dealing with more complex fractions or when you're more comfortable working with decimals.
Steps:
-
Divide the Numerator by the Denominator:
- For 3/4: 3 ÷ 4 = 0.75
- For 5/8: 5 ÷ 8 = 0.625
-
Compare the Decimal Values: We now compare 0.75 and 0.625. Since 0.75 > 0.625, we conclude that 3/4 > 5/8.
Method 3: Visual Representation
For a more intuitive understanding, especially for visual learners, consider representing the fractions graphically. Imagine a circle or a rectangle divided into equal parts.
Steps:
-
Represent 3/4: Draw a circle divided into four equal parts, and shade three of them.
-
Represent 5/8: Draw another circle divided into eight equal parts, and shade five of them.
-
Visual Comparison: By visually comparing the shaded areas of both circles, you can clearly see that the shaded area representing 3/4 is larger than the shaded area representing 5/8. Therefore, 3/4 > 5/8.
Method 4: Cross-Multiplication
This method provides a quick and efficient way to compare fractions without finding a common denominator.
Steps:
-
Cross-Multiply: Multiply the numerator of the first fraction by the denominator of the second fraction, and vice versa.
- 3 x 8 = 24
- 5 x 4 = 20
-
Compare the Products: Compare the two products. Since 24 > 20, we conclude that 3/4 > 5/8.
Why Understanding Fraction Comparison is Important
Mastering fraction comparison is not merely an academic exercise; it has far-reaching implications in various aspects of life:
- Everyday Calculations: From baking (measuring ingredients) to DIY projects (measuring materials), comparing fractions is crucial for accuracy.
- Financial Literacy: Understanding fractions is essential for comprehending percentages, interest rates, and other financial concepts.
- Advanced Mathematics: Fraction comparison forms the foundation for more complex mathematical operations involving fractions, ratios, and proportions.
- Problem-Solving: Many real-world problems involve comparing parts to a whole, requiring a strong understanding of fractions.
Beyond the Basics: Working with Mixed Numbers and Improper Fractions
The methods discussed above can be extended to compare mixed numbers (numbers containing a whole number and a fraction) and improper fractions (fractions where the numerator is greater than or equal to the denominator).
Mixed Numbers: To compare mixed numbers, first convert them into improper fractions, then apply any of the methods discussed above.
Improper Fractions: These can be compared directly using any of the methods. However, converting them to mixed numbers might sometimes simplify the comparison.
Addressing Potential Challenges and Misconceptions
One common misconception is that simply comparing the numerators or denominators is sufficient. This is incorrect, as it ignores the relative sizes of the parts. Always use one of the methods outlined above for accurate comparison.
Conclusion: 3/4 Triumphs!
Through various methods, we have conclusively demonstrated that 3/4 is indeed bigger than 5/8. This seemingly simple comparison serves as a gateway to understanding more complex mathematical concepts, emphasizing the importance of a strong foundation in fraction manipulation and comparison. By mastering these techniques, you'll be well-equipped to tackle a wide range of mathematical problems and real-world applications. Remember to practice regularly and choose the method that best suits your understanding and the complexity of the problem at hand. The more you practice, the more intuitive and effortless fraction comparison will become.
Latest Posts
Latest Posts
-
4 2 9 As An Improper Fraction
May 11, 2025
-
2 Out Of 15 Is What Percent
May 11, 2025
-
How Far Is A 200 Meter Run
May 11, 2025
-
Does A Mother Dog Have A Favorite Puppy
May 11, 2025
-
Which Expression Represents 4 Times As Much As 12
May 11, 2025
Related Post
Thank you for visiting our website which covers about Is 3 4 Bigger Than 5 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.