Is 3 8 Larger Than 5 8
Arias News
May 12, 2025 · 5 min read
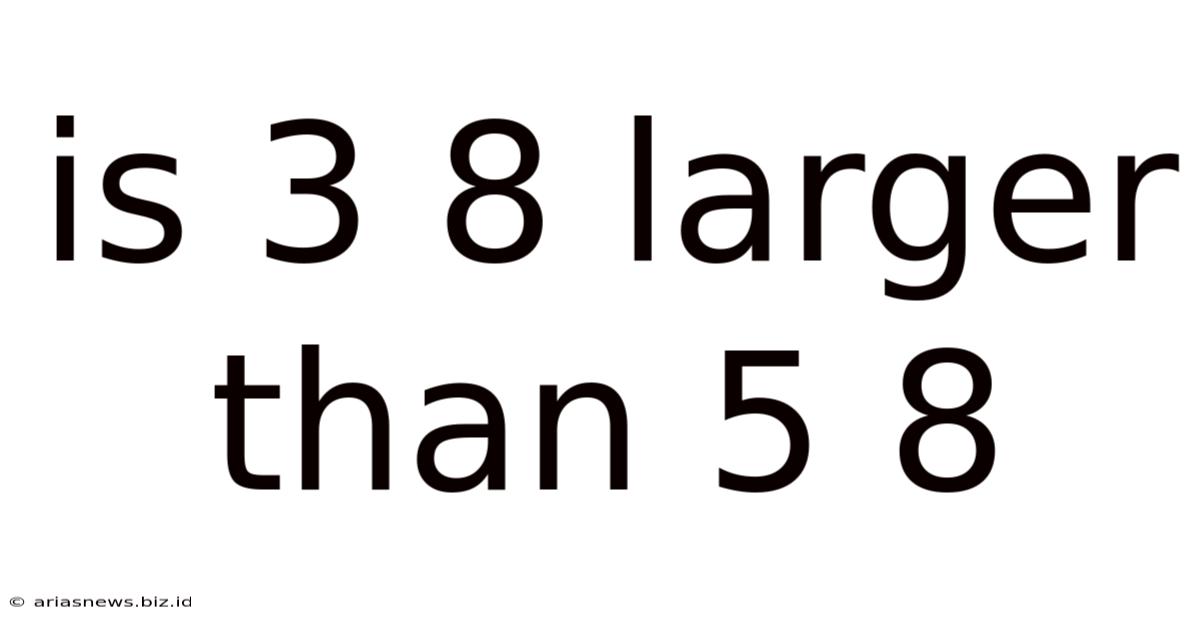
Table of Contents
Is 3/8 Larger Than 5/8? Understanding Fraction Comparison
The question, "Is 3/8 larger than 5/8?" might seem simple at first glance, particularly for those comfortable with fractions. However, understanding the underlying concepts of fraction comparison is crucial for developing a strong foundation in mathematics and problem-solving. This comprehensive guide will not only answer the question definitively but will also delve into various methods for comparing fractions, equipping you with the skills to tackle similar problems confidently.
Understanding Fractions: A Quick Refresher
Before diving into the comparison, let's revisit the fundamental components of a fraction: the numerator and the denominator. The numerator represents the number of parts we have, while the denominator represents the total number of equal parts the whole is divided into. In the fractions 3/8 and 5/8, 8 is the denominator (indicating the whole is divided into eight equal parts), and 3 and 5 are the numerators (representing the number of parts we are considering).
Visualizing Fractions
A powerful technique for understanding fractions is to visualize them. Imagine a pizza cut into eight equal slices. The fraction 3/8 represents three of those slices, while 5/8 represents five slices. By visualizing this, it becomes immediately apparent that 5/8 is larger than 3/8.
Comparing Fractions with the Same Denominator
When comparing fractions with the same denominator (as in our case), the comparison becomes straightforward. The fraction with the larger numerator is the larger fraction. Since 5 is greater than 3, 5/8 is larger than 3/8. This is a fundamental rule for fraction comparison, applicable in many mathematical scenarios.
Alternative Methods for Comparing Fractions
While the method above is the most direct for fractions with identical denominators, let's explore alternative methods applicable to various fraction comparison scenarios. These methods are especially useful when dealing with fractions that have different denominators.
Method 1: Finding a Common Denominator
If you're comparing fractions with different denominators, finding a common denominator is a common approach. This involves finding a multiple of both denominators and then rewriting the fractions with this new denominator. Let's illustrate with an example:
Compare 2/3 and 3/5.
The least common multiple (LCM) of 3 and 5 is 15. We rewrite the fractions:
- 2/3 = (2 x 5) / (3 x 5) = 10/15
- 3/5 = (3 x 3) / (5 x 3) = 9/15
Now, we can easily compare: 10/15 > 9/15, therefore 2/3 > 3/5.
Method 2: Converting to Decimals
Another approach is to convert the fractions into decimals. This is achieved by dividing the numerator by the denominator. For instance:
- 3/8 = 0.375
- 5/8 = 0.625
Comparing the decimal values, it's evident that 0.625 > 0.375, confirming that 5/8 > 3/8. This method is particularly useful when dealing with complex fractions or when performing calculations that require decimal values.
Method 3: Cross-Multiplication
Cross-multiplication offers a convenient method for comparing two fractions. Let's compare a/b and c/d:
- Multiply a by d (ad)
- Multiply c by b (cb)
If ad > cb, then a/b > c/d. If ad < cb, then a/b < c/d. If ad = cb, then a/b = c/d.
Let's apply this to our original problem:
Compare 3/8 and 5/8:
- 3 x 8 = 24
- 5 x 8 = 40
Since 40 > 24, 5/8 > 3/8.
Practical Applications of Fraction Comparison
Understanding fraction comparison is not merely an academic exercise; it has numerous practical applications in various fields:
Cooking and Baking
Recipes often require precise measurements, and comparing fractions is essential for understanding the relative quantities of ingredients. For example, determining whether 1/2 cup of sugar is more or less than 3/4 cup of sugar is crucial for baking success.
Construction and Engineering
Accurate measurements are paramount in construction and engineering. Comparing fractions helps ensure the precise dimensions of structures and components, contributing to structural integrity and safety.
Finance and Budgeting
Managing finances involves dealing with portions and percentages, often represented as fractions. Comparing fractions helps in understanding proportions of income, expenses, and investments.
Data Analysis
In various data analysis scenarios, data is often represented as fractions or proportions. Comparing fractions allows for meaningful interpretation and comparison of data points.
Common Mistakes to Avoid When Comparing Fractions
Several common pitfalls can lead to incorrect conclusions when comparing fractions:
Focusing Solely on Numerators or Denominators
It's crucial to consider both the numerator and the denominator when comparing fractions. Simply comparing numerators or denominators without considering the other component will often lead to inaccurate results.
Incorrectly Applying Cross-Multiplication
When using cross-multiplication, make sure you multiply correctly and compare the resulting products accurately. A simple arithmetic error can lead to an incorrect comparison.
Forgetting to Simplify Fractions
Simplifying fractions before comparison can make the comparison much easier. Always simplify fractions to their lowest terms before proceeding with comparison methods.
Conclusion: Mastering Fraction Comparison
This in-depth exploration of fraction comparison has not only answered the initial question – definitively demonstrating that 5/8 is larger than 3/8 – but has also provided a comprehensive toolkit for tackling various fraction comparison problems. By mastering these methods, you will develop a stronger mathematical foundation and enhance your problem-solving abilities across a wide range of applications. Remember to visualize, utilize common denominators, convert to decimals, or use cross-multiplication, depending on the context and your personal preference. With practice and a solid understanding of these techniques, you can confidently tackle any fraction comparison challenge that comes your way. The key is consistent practice and understanding the underlying logic behind each method. So, grab a pizza, divide it into sections, and start practicing! You'll be a fraction comparison expert in no time.
Latest Posts
Latest Posts
-
What Side Does The Napkin Go On A Place Setting
May 12, 2025
-
Gifts That Begin With The Letter Y
May 12, 2025
-
A House Of A Rabbit Is Called
May 12, 2025
-
How Many Oz Is A Sweet Potato
May 12, 2025
-
Lines That Form Right Angles At Their Point Of Intersection
May 12, 2025
Related Post
Thank you for visiting our website which covers about Is 3 8 Larger Than 5 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.