Is -3 A Rational Number Yes Or No
Arias News
May 10, 2025 · 4 min read
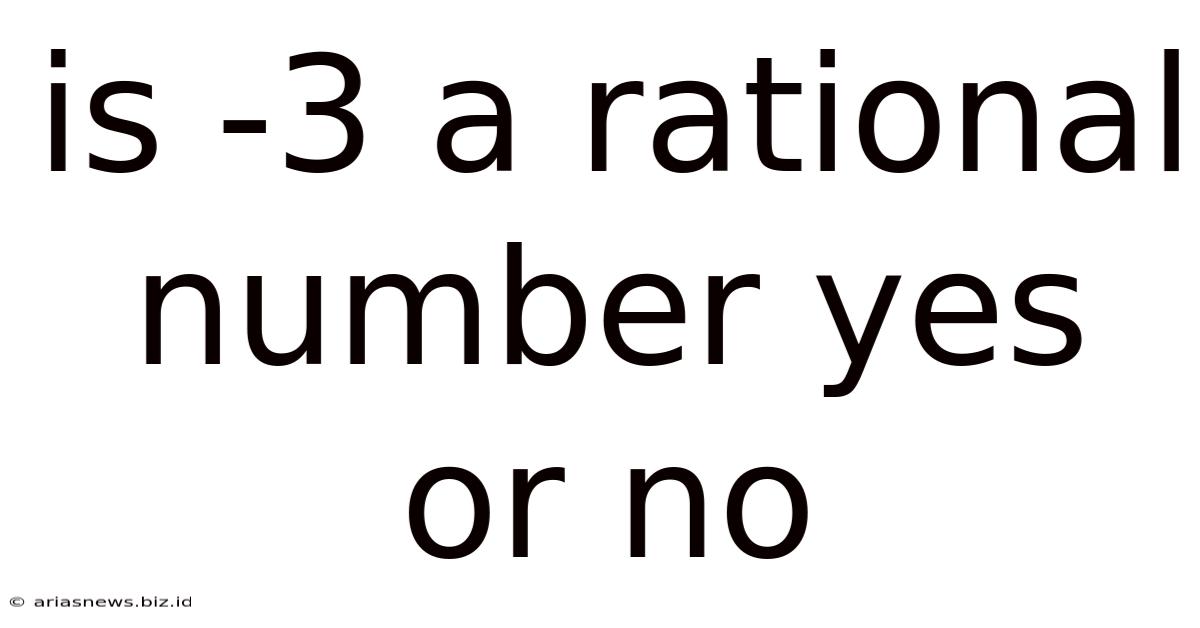
Table of Contents
Is -3 a Rational Number? Yes or No: A Deep Dive into Rational Numbers
The question, "Is -3 a rational number?" might seem simple at first glance. However, understanding the answer requires a firm grasp of the definition of rational numbers and the properties of the number system. This article will delve deep into the concept of rational numbers, explore why -3 fits the definition, and address common misconceptions. We'll also explore related concepts to build a comprehensive understanding.
What are Rational Numbers?
Before we determine if -3 is a rational number, let's define what constitutes a rational number. A rational number is any number that can be expressed as a fraction p/q, where 'p' and 'q' are integers, and 'q' is not equal to zero (q≠0). This seemingly simple definition encompasses a vast range of numbers.
Key Characteristics of Rational Numbers:
-
Integers: All integers (…-3, -2, -1, 0, 1, 2, 3…) are rational numbers. This is because any integer 'p' can be written as p/1, fulfilling the definition of a rational number.
-
Fractions: Fractions, such as 1/2, 3/4, or -5/7, are quintessential examples of rational numbers. They explicitly adhere to the p/q format.
-
Terminating Decimals: Decimals that terminate (end) are rational. For example, 0.75 can be expressed as 3/4. Similarly, 0.25 is equivalent to 1/4.
-
Repeating Decimals: Decimals with repeating patterns (like 0.333… or 0.142857142857…) are also rational. These repeating decimals can be converted into fractions using algebraic techniques. For instance, 0.333… is equal to 1/3.
Why -3 is a Rational Number
Now, let's address the central question: Is -3 a rational number? The answer is a resounding yes. Here's why:
-3 can be expressed as a fraction: -3/1.
This fits the definition perfectly:
- -3 is an integer (our 'p').
- 1 is an integer (our 'q'), and it's not zero.
Therefore, -3 satisfies all the conditions required to be classified as a rational number. It's a simple yet crucial example that demonstrates how integers are a subset of rational numbers.
Exploring Related Concepts: Irrational and Real Numbers
To fully appreciate the significance of -3 being a rational number, let's briefly explore related number systems:
Irrational Numbers:
Irrational numbers are numbers that cannot be expressed as a fraction of two integers. These numbers have decimal representations that neither terminate nor repeat. Famous examples include:
- π (Pi): Approximately 3.14159…, the ratio of a circle's circumference to its diameter.
- e (Euler's number): Approximately 2.71828…, the base of the natural logarithm.
- √2 (Square root of 2): Approximately 1.41421…, a number whose square is 2.
Real Numbers:
Real numbers encompass both rational and irrational numbers. They represent all the numbers on the number line, extending infinitely in both positive and negative directions. Essentially, the real numbers are the union of rational and irrational numbers.
Therefore, -3 is not only a rational number but also a real number. It occupies a specific point on the real number line.
Common Misconceptions about Rational Numbers
While the concept of rational numbers is relatively straightforward, some common misconceptions can lead to confusion:
Misconception 1: Only positive numbers can be rational.
This is incorrect. Rational numbers can be positive, negative, or zero. The key is the ability to express the number as a fraction p/q, where p and q are integers and q≠0.
Misconception 2: All decimals are irrational.
This is false. As discussed earlier, both terminating and repeating decimals are rational. Only non-terminating, non-repeating decimals are irrational.
Misconception 3: A number must be a fraction to be rational.
While a fraction is a clear representation of a rational number, it's not the only representation. Integers are also rational numbers because they can be expressed as fractions (e.g., 5 can be written as 5/1).
Practical Applications of Understanding Rational Numbers
Understanding rational numbers is fundamental to various areas of mathematics and beyond:
- Algebra: Solving equations and inequalities often involves working with rational numbers.
- Calculus: Limits, derivatives, and integrals frequently use rational numbers in their calculations.
- Geometry: Calculating areas, volumes, and other geometric properties often involve rational numbers.
- Computer Science: Representing numbers in computer systems often relies on rational number approximations.
- Engineering and Physics: Many engineering and physics formulas involve rational numbers and fractions.
Conclusion: The Definitive Answer
To reiterate, the answer to the question "Is -3 a rational number?" is definitively yes. -3 fulfills the definition of a rational number because it can be expressed as the fraction -3/1, where both the numerator and the denominator are integers, and the denominator is not zero. Understanding this fundamental concept is crucial for building a strong foundation in mathematics and appreciating the structure of the number system. By grasping the core principles of rational numbers and their relationship to other number sets, you can unlock a deeper understanding of mathematical concepts and their real-world applications.
Latest Posts
Latest Posts
-
How Many Grams Of Protein In 8 Ounces Of Chicken
May 10, 2025
-
How Tall Is 1 52 M In Feet
May 10, 2025
-
What Is Difference Between Vertical And Horizontal
May 10, 2025
-
How Many Servings In A Half Gallon Of Ice Cream
May 10, 2025
-
How Do You Spell 16 In Spanish
May 10, 2025
Related Post
Thank you for visiting our website which covers about Is -3 A Rational Number Yes Or No . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.