Is 83 A Prime Or Composite Number
Arias News
Mar 31, 2025 · 5 min read
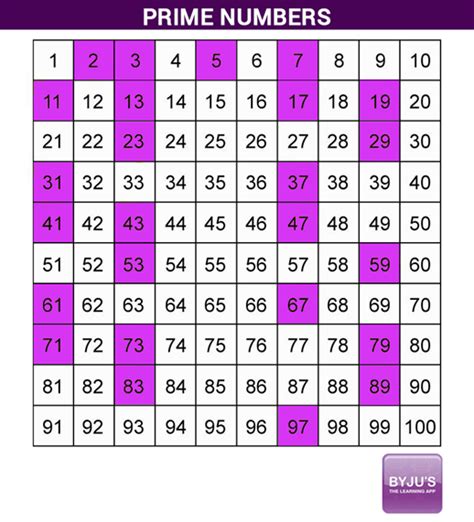
Table of Contents
Is 83 a Prime or Composite Number? A Deep Dive into Prime Numbers and Divisibility
Determining whether a number is prime or composite is a fundamental concept in number theory. While seemingly simple for smaller numbers, the question of primality can become surprisingly complex as numbers grow larger. This article will delve into the question: Is 83 a prime or composite number? We'll explore the definitions of prime and composite numbers, examine methods for determining primality, and apply these methods to the number 83. Beyond 83, we'll also discuss the significance of prime numbers in mathematics and their applications in cryptography and other fields.
Understanding Prime and Composite Numbers
Before we tackle 83, let's establish a clear understanding of the terms "prime" and "composite."
Prime Numbers: A prime number is a natural number greater than 1 that has only two distinct positive divisors: 1 and itself. This means it's not divisible by any other whole number without leaving a remainder. Examples of prime numbers include 2, 3, 5, 7, 11, and so on. The number 1 is neither prime nor composite.
Composite Numbers: A composite number is a positive integer that has at least one divisor other than 1 and itself. In other words, it can be factored into smaller whole numbers. Examples include 4 (2 x 2), 6 (2 x 3), 9 (3 x 3), and so on.
Methods for Determining Primality
Several methods exist to determine whether a number is prime or composite. For smaller numbers like 83, a simple approach is sufficient. For larger numbers, more sophisticated algorithms are necessary.
1. Trial Division
This is the most straightforward method. We systematically check for divisibility by all prime numbers less than or equal to the square root of the number in question. If the number is divisible by any of these primes, it's composite. If not, it's prime.
Why the square root? If a number n has a divisor greater than √n, it must also have a divisor smaller than √n. This significantly reduces the number of checks required.
2. Sieve of Eratosthenes
This is an ancient algorithm for finding all prime numbers up to a specified integer. It's efficient for generating lists of primes within a given range.
3. Advanced Primality Tests
For very large numbers, trial division becomes computationally expensive. More sophisticated algorithms, such as the Miller-Rabin primality test and the AKS primality test, are employed. These probabilistic tests offer high accuracy and efficiency for determining primality in large numbers.
Is 83 a Prime or Composite Number?
Now, let's apply our knowledge to the number 83. Using trial division, we need to check for divisibility by prime numbers less than or equal to √83 ≈ 9.1. These primes are 2, 3, 5, and 7.
- Divisibility by 2: 83 is not divisible by 2 (it's odd).
- Divisibility by 3: The sum of the digits of 83 is 8 + 3 = 11, which is not divisible by 3. Therefore, 83 is not divisible by 3.
- Divisibility by 5: 83 does not end in 0 or 5, so it's not divisible by 5.
- Divisibility by 7: 83 divided by 7 leaves a remainder. (83 = 7 x 11 + 6).
Since 83 is not divisible by any of the prime numbers less than or equal to its square root, we conclude that:
83 is a prime number.
The Significance of Prime Numbers
Prime numbers are far more than just interesting mathematical curiosities. They hold profound significance across various branches of mathematics and have crucial applications in other fields:
1. Fundamental Theorem of Arithmetic
The fundamental theorem of arithmetic states that every integer greater than 1 can be represented uniquely as a product of prime numbers. This theorem forms the bedrock of number theory, providing a foundation for many advanced concepts.
2. Cryptography
Prime numbers play a crucial role in modern cryptography. Many widely used encryption algorithms, such as RSA, rely heavily on the difficulty of factoring large composite numbers into their prime factors. The security of these systems depends on the seemingly insurmountable task of finding the prime factors of extremely large numbers.
3. Number Theory Research
Prime numbers are a central topic of ongoing research in number theory. Questions surrounding the distribution of prime numbers, such as the Riemann Hypothesis, are among the most significant unsolved problems in mathematics.
4. Other Applications
Prime numbers find applications in various fields, including:
- Hashing algorithms: Used in data structures and databases.
- Random number generation: Crucial for simulations and other applications requiring randomness.
- Coding theory: Used in error correction and data transmission.
Conclusion: 83 – A Prime Example
We've definitively established that 83 is a prime number. This seemingly simple question provides a gateway to understanding the fascinating world of prime numbers, their properties, and their profound implications across mathematics and computer science. The methods discussed here, from simple trial division to sophisticated algorithms, illustrate the different approaches used to determine primality, highlighting the computational challenges involved as numbers grow larger. The enduring mystery and importance of prime numbers continue to inspire research and innovation, solidifying their position as fundamental building blocks of mathematics and technology. The exploration of primality is not just an academic exercise; it underpins the security of our digital world and fuels ongoing mathematical discovery. Understanding the properties of numbers like 83 allows us to appreciate the elegant simplicity and profound complexity of the mathematical universe.
Latest Posts
Latest Posts
-
How Long Is Miracle Whip Good After Opened
Apr 02, 2025
-
How Many Centimeters Is A Paper Clip
Apr 02, 2025
-
How Many Hours Is 5pm To 1am
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about Is 83 A Prime Or Composite Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
