Is Square Root Of 11 A Rational Number
Arias News
May 12, 2025 · 4 min read
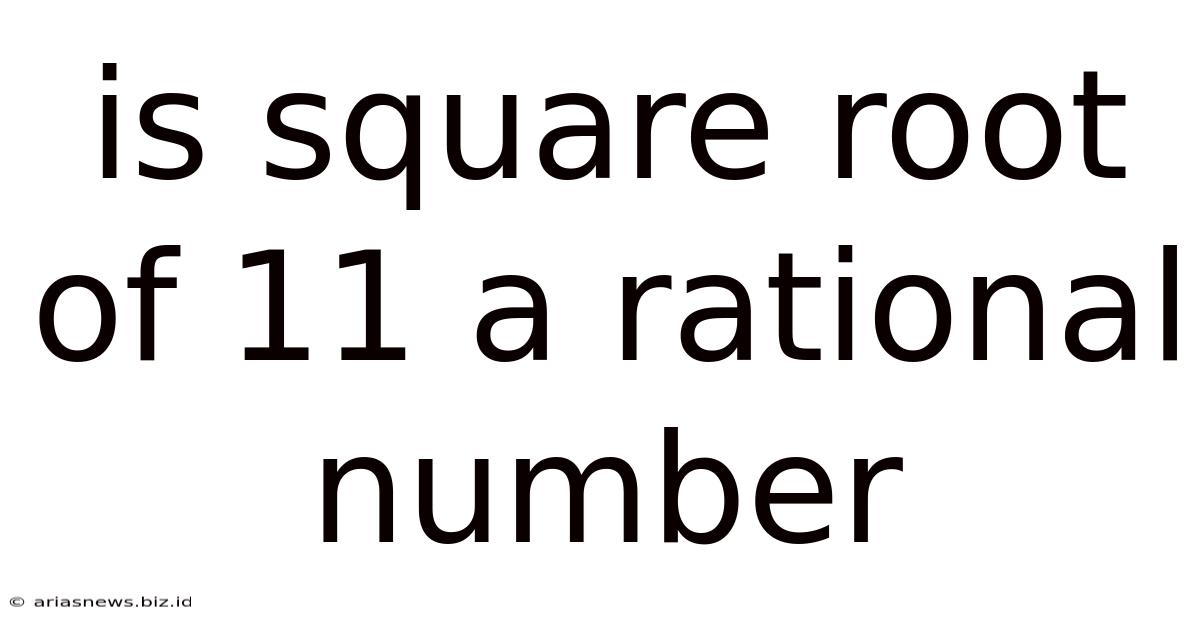
Table of Contents
Is the Square Root of 11 a Rational Number? A Deep Dive into Irrationality
The question of whether the square root of 11 is a rational number is a fundamental one in mathematics, touching upon the core concepts of number theory. The short answer is no, the square root of 11 is not a rational number; it's irrational. But understanding why requires delving into the definitions of rational and irrational numbers and employing a proof technique known as proof by contradiction. This article will explore this topic comprehensively, providing a clear and insightful explanation accessible to a broad audience.
Understanding Rational and Irrational Numbers
Before we tackle the square root of 11, let's solidify our understanding of rational and irrational numbers.
Rational Numbers: A rational number is any number that can be expressed as a fraction p/q, where 'p' and 'q' are integers, and 'q' is not equal to zero. Examples include 1/2, 3/4, -2/5, and even integers like 5 (which can be expressed as 5/1). The decimal representation of a rational number either terminates (like 0.75) or repeats in a predictable pattern (like 0.333...).
Irrational Numbers: Irrational numbers cannot be expressed as a fraction of two integers. Their decimal representations are non-terminating and non-repeating. Famous examples include π (pi), e (Euler's number), and the square root of most non-perfect squares.
Proof by Contradiction: Demonstrating the Irrationality of √11
To prove that √11 is irrational, we'll use a classic mathematical technique called proof by contradiction. This method assumes the opposite of what we want to prove and then shows that this assumption leads to a contradiction, thereby proving the original statement.
Step 1: The Assumption
Let's assume, for the sake of contradiction, that √11 is a rational number. This means we can express it as a fraction p/q, where p and q are integers, q ≠ 0, and the fraction is in its simplest form (meaning p and q share no common factors other than 1).
Step 2: Manipulating the Equation
If √11 = p/q, then squaring both sides gives us:
11 = p²/q²
Rearranging the equation, we get:
11q² = p²
Step 3: Deductions about Divisibility
This equation tells us that p² is divisible by 11. Since 11 is a prime number, this implies that p itself must also be divisible by 11. We can express this as:
p = 11k (where k is an integer)
Substituting this back into the equation 11q² = p², we get:
11q² = (11k)²
11q² = 121k²
Dividing both sides by 11, we obtain:
q² = 11k²
Step 4: The Contradiction
This equation now reveals that q² is also divisible by 11, and therefore, q itself must be divisible by 11.
We've now reached a contradiction. We initially assumed that p/q is in its simplest form, meaning p and q share no common factors. However, our proof shows that both p and q are divisible by 11, implying they do share a common factor. This is a contradiction.
Step 5: The Conclusion
Since our initial assumption (that √11 is rational) leads to a contradiction, the assumption must be false. Therefore, √11 is irrational.
Exploring Further: Generalizing the Proof
The proof above can be generalized to show that the square root of any non-perfect square integer is irrational. The key element is the prime factorization of the integer and the properties of prime numbers within the proof. If the integer is not a perfect square, the same contradiction will arise, demonstrating the irrationality of its square root.
Practical Implications and Applications
While the irrationality of √11 might seem like an abstract mathematical concept, it has practical implications in various fields:
-
Geometry: Calculations involving lengths, areas, and volumes often involve irrational numbers, reflecting the inherent limitations of representing certain geometric relationships with rational numbers alone. For example, calculating the diagonal of a square with side length of 1 involves √2, another irrational number.
-
Engineering and Physics: Many physical phenomena and engineering designs are described by equations involving irrational numbers, often derived from trigonometric functions and geometry. These numbers need to be approximated for practical calculations.
-
Computer Science: Representing irrational numbers in computers requires approximations using floating-point arithmetic. Understanding the limitations of these approximations is crucial in numerical analysis and scientific computing.
-
Number Theory: The study of irrational numbers, including their properties and relationships, forms a significant part of number theory, a branch of mathematics with deep connections to cryptography and other areas.
Approximating Irrational Numbers
Although we can't express irrational numbers exactly as fractions, we can approximate them to any desired degree of accuracy. This is often done using decimal expansions or continued fractions. For √11, the decimal approximation is approximately 3.31662479. This approximation is sufficient for many practical purposes.
Conclusion: The Beauty of Irrationality
The irrationality of √11, and other irrational numbers, highlights the richness and complexity of the number system. It showcases the power of mathematical reasoning and the elegance of proofs like proof by contradiction. While we can't represent them perfectly as fractions, irrational numbers play a crucial role in many aspects of mathematics and its applications, enriching our understanding of the world around us. The seeming simplicity of the question – "Is the square root of 11 a rational number?" – leads to a surprisingly profound exploration of fundamental mathematical principles.
Latest Posts
Related Post
Thank you for visiting our website which covers about Is Square Root Of 11 A Rational Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.