Least Common Denominator Of 7 And 9
Arias News
Mar 30, 2025 · 4 min read
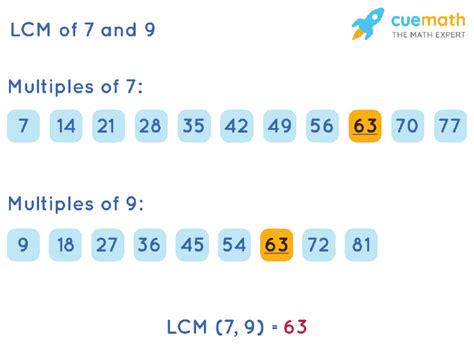
Table of Contents
Finding the Least Common Denominator (LCD) of 7 and 9: A Comprehensive Guide
Finding the least common denominator (LCD) is a fundamental concept in arithmetic, crucial for adding and subtracting fractions. This comprehensive guide will delve into the process of determining the LCD of 7 and 9, exploring multiple methods and explaining the underlying mathematical principles. We'll also touch upon the broader applications of LCDs in various mathematical contexts.
Understanding Least Common Denominator (LCD)
Before we dive into the specifics of finding the LCD of 7 and 9, let's clarify the concept itself. The least common denominator (LCD) of two or more numbers is the smallest positive integer that is a multiple of all the given numbers. In simpler terms, it's the smallest number that all the given numbers can divide into evenly. This concept is pivotal when performing operations on fractions with different denominators. To add or subtract fractions, they must share a common denominator, and the LCD makes this process efficient by using the smallest possible denominator.
Method 1: Listing Multiples
This method is straightforward, particularly useful for smaller numbers like 7 and 9. We list the multiples of each number until we find the smallest common multiple.
Multiples of 7:
7, 14, 21, 28, 35, 42, 49, 56, 63, 70, 77, 84, 91, 98, 105...
Multiples of 9:
9, 18, 27, 36, 45, 54, 63, 72, 81, 90, 99, 108, 117, 126, 135...
By comparing the lists, we find that the smallest number present in both lists is 63. Therefore, the least common denominator of 7 and 9 is 63.
Method 2: Prime Factorization
This method is more efficient for larger numbers and provides a systematic approach. It involves breaking down each number into its prime factors. Prime factors are prime numbers (numbers divisible only by 1 and themselves) that multiply together to give the original number.
Prime Factorization of 7:
7 is a prime number, so its prime factorization is simply 7.
Prime Factorization of 9:
9 = 3 x 3 = 3²
To find the LCD, we take the highest power of each prime factor present in either factorization and multiply them together. In this case, we have 3² and 7.
LCD(7, 9) = 3² x 7 = 9 x 7 = 63
This method confirms our result from the previous method.
Method 3: Using the Formula (For Two Numbers)
For two numbers 'a' and 'b', there's a formula that can be used to find their least common multiple (LCM), which is equivalent to the LCD when working with fractions:
LCM(a, b) = (|a x b|) / GCD(a, b)
Where GCD(a, b) represents the greatest common divisor of 'a' and 'b'.
Finding the GCD of 7 and 9:
The greatest common divisor (GCD) is the largest number that divides both 7 and 9 without leaving a remainder. Since 7 and 9 share only 1 as a common divisor, their GCD is 1.
Applying the Formula:
LCM(7, 9) = (|7 x 9|) / GCD(7, 9) = (63) / 1 = 63
Again, this method confirms the LCD is 63.
Why is the LCD Important?
The LCD is crucial in various mathematical operations and applications:
-
Adding and Subtracting Fractions: The LCD allows us to rewrite fractions with a common denominator, enabling straightforward addition or subtraction of the numerators. For example, adding 1/7 and 2/9 requires finding the LCD (63):
(1/7) x (9/9) + (2/9) x (7/7) = 9/63 + 14/63 = 23/63
-
Comparing Fractions: Determining which fraction is larger or smaller becomes much easier when they share a common denominator.
-
Solving Equations: In algebraic equations involving fractions, finding the LCD is essential for simplifying the equation and solving for the unknown variable.
-
Working with Ratios and Proportions: The LCD can help simplify and solve problems involving ratios and proportions.
-
Real-World Applications: The concept of LCD finds practical applications in various fields such as engineering, construction, and finance, where precise measurements and calculations are crucial.
Advanced Concepts and Extensions
The methods discussed above are applicable to finding the LCD of two numbers. However, the principles can be extended to find the LCD of three or more numbers. For multiple numbers, prime factorization becomes a particularly powerful tool.
Finding the LCD of Multiple Numbers:
Let's find the LCD of 7, 9, and 12.
-
Prime Factorization:
- 7 = 7
- 9 = 3²
- 12 = 2² x 3
-
Determining the LCD: We take the highest power of each prime factor present in any of the factorizations: 2², 3², and 7.
LCD(7, 9, 12) = 2² x 3² x 7 = 4 x 9 x 7 = 252
Conclusion
Finding the least common denominator is a fundamental skill in mathematics. While seemingly simple for smaller numbers, understanding the underlying principles – prime factorization and the relationship between LCM and GCD – becomes crucial when dealing with more complex scenarios involving multiple numbers or larger values. Mastering the LCD is essential for proficiency in arithmetic and forms a cornerstone for more advanced mathematical concepts. The various methods outlined here provide a robust foundation for understanding and calculating LCDs effectively, enabling efficient problem-solving in diverse mathematical contexts. Remember to choose the method most appropriate for the numbers involved, prioritizing efficiency and accuracy.
Latest Posts
Latest Posts
-
How Many Cups Is 18 Oz Of Peanut Butter
Apr 01, 2025
-
Whats The Front Of A Train Called
Apr 01, 2025
-
How Many Blades Of Grass In The World
Apr 01, 2025
-
What Is 1 Trillionth To The 10th Power
Apr 01, 2025
-
How Many Plutos Can Fit In The Sun
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about Least Common Denominator Of 7 And 9 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
