Least Common Multiple Of 10 15 25
Arias News
Mar 28, 2025 · 5 min read
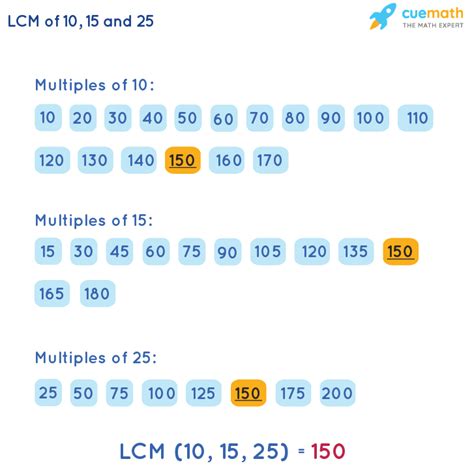
Table of Contents
Finding the Least Common Multiple (LCM) of 10, 15, and 25: A Comprehensive Guide
The least common multiple (LCM) is a fundamental concept in mathematics, particularly in number theory and arithmetic. Understanding how to find the LCM is crucial for various applications, from solving fractional equations to scheduling tasks efficiently. This comprehensive guide will delve deep into calculating the LCM of 10, 15, and 25, exploring different methods and underlying principles. We'll also examine the broader significance of LCMs and their real-world applications.
Understanding Least Common Multiple (LCM)
Before we tackle the specific problem of finding the LCM of 10, 15, and 25, let's solidify our understanding of what an LCM actually is. The least common multiple of two or more integers is the smallest positive integer that is divisible by all the given integers. In simpler terms, it's the smallest number that all the numbers in the set can divide into without leaving a remainder.
For example, let's consider the numbers 2 and 3. Multiples of 2 are 2, 4, 6, 8, 10, and so on. Multiples of 3 are 3, 6, 9, 12, 15, and so on. The common multiples of 2 and 3 are 6, 12, 18, etc. The smallest of these common multiples is 6, therefore, the LCM of 2 and 3 is 6.
Method 1: Prime Factorization Method
This is arguably the most common and reliable method for finding the LCM, especially when dealing with larger numbers or a larger set of numbers. The prime factorization method involves breaking down each number into its prime factors – the prime numbers that multiply together to make the original number.
Step 1: Prime Factorization
Let's find the prime factorization of 10, 15, and 25:
- 10: 2 x 5
- 15: 3 x 5
- 25: 5 x 5 or 5²
Step 2: Identify the Highest Power of Each Prime Factor
Now, we identify the highest power of each prime factor present in the factorizations:
- The prime factor 2 appears only once (in the factorization of 10).
- The prime factor 3 appears only once (in the factorization of 15).
- The prime factor 5 appears twice (in the factorization of 25, as 5²).
Step 3: Multiply the Highest Powers
Finally, we multiply these highest powers together to obtain the LCM:
LCM(10, 15, 25) = 2 x 3 x 5² = 2 x 3 x 25 = 150
Therefore, the least common multiple of 10, 15, and 25 is 150. This means 150 is the smallest positive integer that is divisible by 10, 15, and 25 without leaving a remainder.
Method 2: Listing Multiples Method
This method is straightforward but can be less efficient for larger numbers. It involves listing the multiples of each number until you find the smallest common multiple.
Step 1: List Multiples
Let's list the multiples of 10, 15, and 25:
- Multiples of 10: 10, 20, 30, 40, 50, 60, 70, 80, 90, 100, 110, 120, 130, 140, 150, ...
- Multiples of 15: 15, 30, 45, 60, 75, 90, 105, 120, 135, 150, ...
- Multiples of 25: 25, 50, 75, 100, 125, 150, ...
Step 2: Identify the Smallest Common Multiple
By comparing the lists, we can see that the smallest common multiple of 10, 15, and 25 is 150.
This method is less efficient for larger numbers, as listing all multiples can become quite time-consuming. The prime factorization method is generally preferred for its efficiency and clarity.
Method 3: Using the Greatest Common Divisor (GCD)
The LCM and the greatest common divisor (GCD) are closely related. There's a formula that links them:
LCM(a, b) * GCD(a, b) = a * b
This formula can be extended to more than two numbers, though the calculation becomes more complex. While this method can be used, it's often more efficient to use prime factorization directly, especially for three or more numbers.
Real-World Applications of LCM
The concept of LCM has numerous practical applications in everyday life and various fields:
- Scheduling: Imagine you have three tasks to perform – one that repeats every 10 days, one every 15 days, and another every 25 days. To determine when all three tasks will coincide, you need to find the LCM (150 days).
- Fractions: When adding or subtracting fractions, you need a common denominator – which is the LCM of the denominators.
- Gear Ratios: In engineering, gear ratios often involve finding the LCM to synchronize rotations.
- Music: The LCM plays a role in understanding musical intervals and harmonies.
- Construction and Engineering: In construction and other engineering fields, LCM is utilized to determine the optimal timing of various stages in a project or in coordinating the operation of machinery. For example, you might need to synchronize conveyor belts with different cycle times.
Beyond the Basics: Extending the Concept
The methods described above can be extended to find the LCM of more than three numbers. The prime factorization method remains the most efficient approach. Simply factorize each number, identify the highest power of each prime factor present across all numbers, and multiply those highest powers together.
For example, to find the LCM of 10, 15, 25, and 30:
-
Prime Factorization:
- 10 = 2 x 5
- 15 = 3 x 5
- 25 = 5 x 5 = 5²
- 30 = 2 x 3 x 5
-
Highest Powers:
- 2¹
- 3¹
- 5²
-
Multiply: LCM(10, 15, 25, 30) = 2 x 3 x 5² = 150
Conclusion: Mastering LCM Calculations
Understanding and calculating the least common multiple is an essential skill with wide-ranging applications. The prime factorization method offers the most efficient and reliable approach, especially when dealing with multiple numbers or larger values. By mastering this concept, you enhance your problem-solving abilities in various mathematical and real-world scenarios. Remember, practice is key! Try working through different examples to solidify your understanding and become proficient in LCM calculations. The ability to quickly and accurately determine the LCM will prove invaluable in numerous contexts.
Latest Posts
Latest Posts
-
How Much Does A Cubic Foot Of Soil Weigh
Mar 31, 2025
-
How Many Square Feet In 28 Acres
Mar 31, 2025
-
Can You Touch Elf On The Shelf On Christmas Eve
Mar 31, 2025
-
How Many Ounces In Pint Of Sour Cream
Mar 31, 2025
-
Harry Potter Goblet Of Fire Ar Answers
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about Least Common Multiple Of 10 15 25 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
