Least Common Multiple Of 12 And 15
Arias News
Apr 06, 2025 · 5 min read
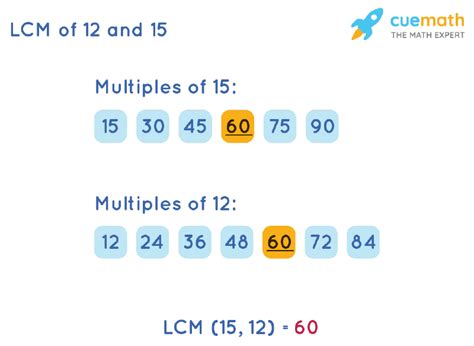
Table of Contents
Finding the Least Common Multiple (LCM) of 12 and 15: A Comprehensive Guide
The least common multiple (LCM) is a fundamental concept in mathematics, particularly in number theory and arithmetic. Understanding how to calculate the LCM is crucial for various applications, ranging from simple fraction operations to more complex problems in algebra and beyond. This comprehensive guide will explore the LCM of 12 and 15, detailing multiple methods for calculation and highlighting the broader significance of this mathematical concept.
What is the Least Common Multiple (LCM)?
The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the integers. In simpler terms, it's the smallest number that contains all the numbers as factors. For example, the LCM of 2 and 3 is 6 because 6 is the smallest number divisible by both 2 and 3.
Methods for Finding the LCM of 12 and 15
Several methods can be used to determine the LCM of 12 and 15. Let's explore the most common approaches:
1. Listing Multiples Method
This is a straightforward method, especially for smaller numbers. We list the multiples of each number until we find the smallest multiple common to both.
Multiples of 12: 12, 24, 36, 48, 60, 72, 84, 96, 108, 120, ...
Multiples of 15: 15, 30, 45, 60, 75, 90, 105, 120, ...
By comparing the lists, we see that the smallest common multiple is 60. Therefore, the LCM(12, 15) = 60.
This method is simple but can become cumbersome for larger numbers.
2. Prime Factorization Method
This is a more efficient method, particularly for larger numbers. It involves finding the prime factorization of each number and then constructing the LCM from the prime factors.
Prime factorization of 12: 2² × 3
Prime factorization of 15: 3 × 5
To find the LCM, we take the highest power of each prime factor present in either factorization:
- The highest power of 2 is 2² = 4
- The highest power of 3 is 3¹ = 3
- The highest power of 5 is 5¹ = 5
Multiplying these highest powers together gives us the LCM: 4 × 3 × 5 = 60. Therefore, LCM(12, 15) = 60.
This method is generally preferred for its efficiency and systematic approach.
3. Greatest Common Divisor (GCD) Method
The LCM and GCD (greatest common divisor) of two numbers are related by the following formula:
LCM(a, b) × GCD(a, b) = a × b
First, we need to find the GCD of 12 and 15. We can use the Euclidean algorithm for this:
- Divide 15 by 12: 15 = 12 × 1 + 3
- Divide 12 by the remainder 3: 12 = 3 × 4 + 0
The last non-zero remainder is 3, so GCD(12, 15) = 3.
Now, we can use the formula:
LCM(12, 15) = (12 × 15) / GCD(12, 15) = (180) / 3 = 60
Therefore, LCM(12, 15) = 60. This method is also efficient and relies on a well-established algorithm for finding the GCD.
Applications of LCM
The LCM has numerous applications across various mathematical fields and real-world scenarios. Here are some examples:
-
Adding and Subtracting Fractions: Finding a common denominator when adding or subtracting fractions involves determining the LCM of the denominators. For instance, to add 1/12 and 1/15, we find the LCM of 12 and 15 (which is 60), convert the fractions to equivalent fractions with a denominator of 60, and then add them.
-
Scheduling and Cycles: The LCM is useful in solving problems involving repeating events or cycles. For example, if two machines operate on cycles of 12 and 15 minutes respectively, the LCM (60 minutes) represents the time it takes for both machines to complete a cycle simultaneously.
-
Modular Arithmetic: The LCM plays a significant role in modular arithmetic, which deals with remainders after division.
-
Music Theory: In music theory, the LCM is used to determine the least common multiple of the lengths of notes, which is helpful in understanding rhythm and harmony.
-
Computer Science: The concept of LCM finds application in various algorithms and data structures.
Understanding the Relationship Between LCM and GCD
The LCM and GCD are intimately related. As shown earlier, their product equals the product of the two numbers:
LCM(a, b) × GCD(a, b) = a × b
This relationship is a fundamental property and provides an alternative method for calculating the LCM if the GCD is known.
LCM of More Than Two Numbers
The concepts discussed above can be extended to find the LCM of more than two numbers. The prime factorization method remains particularly useful in these cases. We find the prime factorization of each number, and the LCM is the product of the highest powers of all prime factors present in any of the factorizations.
For instance, to find the LCM of 12, 15, and 20:
- Prime factorization of 12: 2² × 3
- Prime factorization of 15: 3 × 5
- Prime factorization of 20: 2² × 5
The LCM is 2² × 3 × 5 = 60.
Conclusion
The least common multiple is a fundamental concept with significant applications in various mathematical and practical contexts. Understanding the different methods for calculating the LCM – listing multiples, prime factorization, and the GCD method – equips one with the tools to tackle problems involving this crucial mathematical concept. The relationship between the LCM and GCD provides further insight into the underlying structure of numbers and enhances our ability to solve problems efficiently. Mastering the LCM is a key step in developing a stronger foundation in mathematics.
Latest Posts
Latest Posts
-
Unit 13 Vocabulary Workshop Level C Answers
Apr 07, 2025
-
How To Blow Up A Whoopee Cushion
Apr 07, 2025
-
How Much Is 2 Oz Of Sausage
Apr 07, 2025
-
What Is The Difference Between Poetry And Prose
Apr 07, 2025
-
How Much Ml Is In A Water Bottle
Apr 07, 2025
Related Post
Thank you for visiting our website which covers about Least Common Multiple Of 12 And 15 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.