Least Common Multiple Of 9 12 18
Arias News
May 11, 2025 · 5 min read
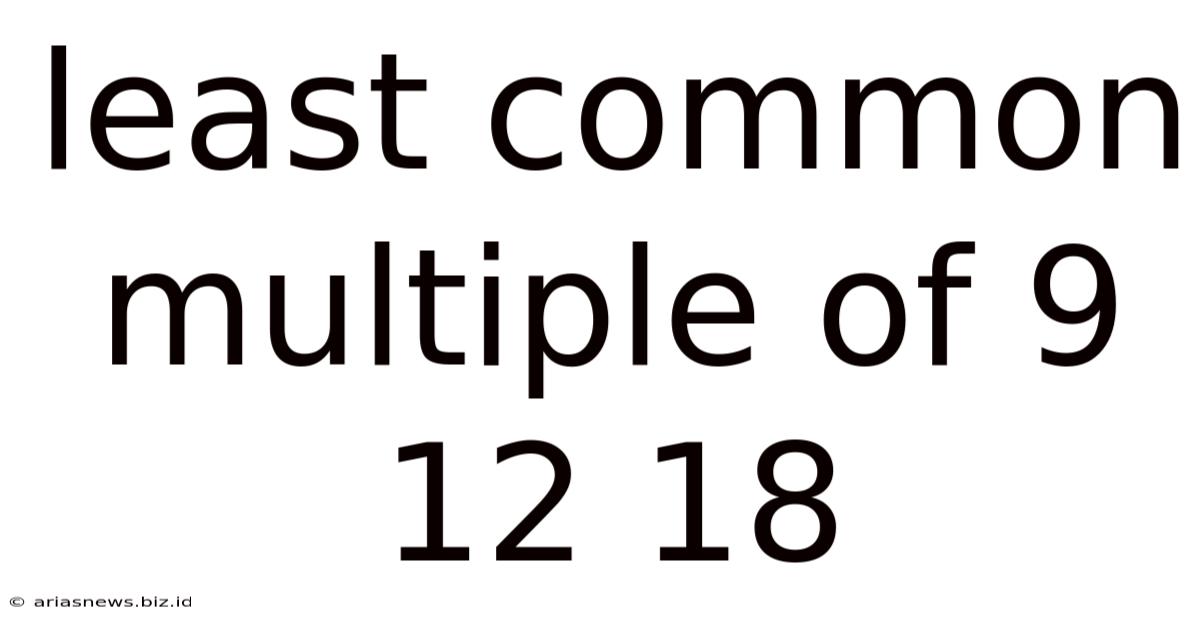
Table of Contents
Finding the Least Common Multiple (LCM) of 9, 12, and 18: A Comprehensive Guide
The least common multiple (LCM) is a fundamental concept in mathematics, particularly in number theory and arithmetic. Understanding how to find the LCM is crucial for various applications, from simplifying fractions to solving problems involving periodic events. This article delves into the process of calculating the LCM of 9, 12, and 18, explaining multiple methods and providing a comprehensive understanding of the underlying principles. We'll also explore the broader implications of LCM and its real-world applications.
Understanding the Least Common Multiple (LCM)
The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the integers. In simpler terms, it's the smallest number that all the given numbers can divide into evenly without leaving a remainder. This concept is distinct from the greatest common divisor (GCD), which is the largest number that divides all the given integers without leaving a remainder.
Finding the LCM is useful in various situations, such as:
- Fraction addition and subtraction: Finding a common denominator when adding or subtracting fractions requires finding the LCM of the denominators.
- Scheduling problems: Determining when events with different periodicities will occur simultaneously (e.g., buses arriving at a stop).
- Modular arithmetic: Solving congruences and other problems involving modular arithmetic often involve finding the LCM.
- Measurement conversions: Converting between units with different common multiples.
Methods for Finding the LCM of 9, 12, and 18
Several methods exist for calculating the LCM of a set of numbers. Let's explore the most common ones, applying them to find the LCM of 9, 12, and 18.
Method 1: Listing Multiples
This method is straightforward but can be time-consuming for larger numbers. We list the multiples of each number until we find the smallest multiple common to all three:
- Multiples of 9: 9, 18, 27, 36, 45, 54, 72, 81, 90, 108...
- Multiples of 12: 12, 24, 36, 48, 60, 72, 84, 96, 108...
- Multiples of 18: 18, 36, 54, 72, 90, 108...
By comparing the lists, we see that the smallest common multiple is 36. However, this becomes less efficient with larger numbers.
Method 2: Prime Factorization
This is a more efficient method, especially for larger numbers. It involves finding the prime factorization of each number and then constructing the LCM from the prime factors.
-
Find the prime factorization of each number:
- 9 = 3²
- 12 = 2² × 3
- 18 = 2 × 3²
-
Identify the highest power of each prime factor:
- The highest power of 2 is 2² = 4
- The highest power of 3 is 3² = 9
-
Multiply the highest powers together:
- LCM(9, 12, 18) = 2² × 3² = 4 × 9 = 36
Therefore, the LCM of 9, 12, and 18 is 36. This method is generally preferred for its efficiency and systematic approach.
Method 3: Using the GCD (Greatest Common Divisor)
The LCM and GCD are related by the following formula:
LCM(a, b) × GCD(a, b) = a × b
While this formula is typically used for two numbers, we can extend it to multiple numbers by finding the LCM iteratively.
-
Find the GCD of 9 and 12: The GCD(9, 12) = 3.
-
Find the LCM of 9 and 12 using the formula: LCM(9, 12) = (9 × 12) / GCD(9, 12) = 108 / 3 = 36
-
Find the GCD of 36 and 18: GCD(36, 18) = 18
-
Find the LCM of 36 and 18 using the formula: LCM(36, 18) = (36 × 18) / GCD(36, 18) = 648 / 18 = 36
Therefore, the LCM of 9, 12, and 18 is 36. This method highlights the relationship between LCM and GCD.
Real-World Applications of LCM
The concept of LCM extends beyond theoretical mathematics and finds practical applications in various real-world scenarios.
Scheduling and Synchronization
Imagine three machines in a factory operating on different cycles: Machine A completes a cycle every 9 minutes, Machine B every 12 minutes, and Machine C every 18 minutes. To determine when all three machines will complete a cycle simultaneously, we need to find the LCM(9, 12, 18) = 36. This means all three machines will complete a cycle together every 36 minutes.
Fraction Arithmetic
When adding or subtracting fractions, we must find a common denominator, which is the LCM of the denominators. For example, to add 1/9 + 1/12 + 1/18, we need to find the LCM of 9, 12, and 18, which is 36. We then rewrite the fractions with a denominator of 36:
4/36 + 3/36 + 2/36 = 9/36 = 1/4
Pattern Recognition and Repetition
LCM is useful in identifying repeating patterns and cycles. Consider a repeating sequence of events or a periodic phenomenon. The LCM helps determine when the pattern will repeat itself completely.
Expanding the Concept: LCM for More Than Three Numbers
The methods described above can be extended to find the LCM of more than three numbers. The prime factorization method remains the most efficient. For example, to find the LCM of 9, 12, 18, and 24:
-
Prime Factorization:
- 9 = 3²
- 12 = 2² × 3
- 18 = 2 × 3²
- 24 = 2³ × 3
-
Highest Powers:
- Highest power of 2: 2³ = 8
- Highest power of 3: 3² = 9
-
Multiply:
- LCM(9, 12, 18, 24) = 2³ × 3² = 8 × 9 = 72
Conclusion
Finding the least common multiple is a crucial skill in mathematics with far-reaching applications. While simple listing works for small numbers, the prime factorization method provides a more efficient and systematic approach, especially when dealing with larger numbers or a greater number of integers. Understanding LCM allows for the solution of problems related to scheduling, fraction simplification, and pattern recognition in various fields. The relationship between LCM and GCD further enriches the understanding of these fundamental mathematical concepts. Mastering the calculation of LCM opens doors to solving a wide range of problems in both theoretical and applied mathematics.
Latest Posts
Latest Posts
-
Does Chicken Float When Its Done Frying
May 11, 2025
-
Cost Of An Oil Change At Firestone
May 11, 2025
-
If You Fail A Final Do You Fail The Class
May 11, 2025
-
Looking Forward To Doing Business With You
May 11, 2025
-
How Much Should A 12 Year Old Bench
May 11, 2025
Related Post
Thank you for visiting our website which covers about Least Common Multiple Of 9 12 18 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.