Least Common Multiple Of 9 And 16
Arias News
May 10, 2025 · 4 min read
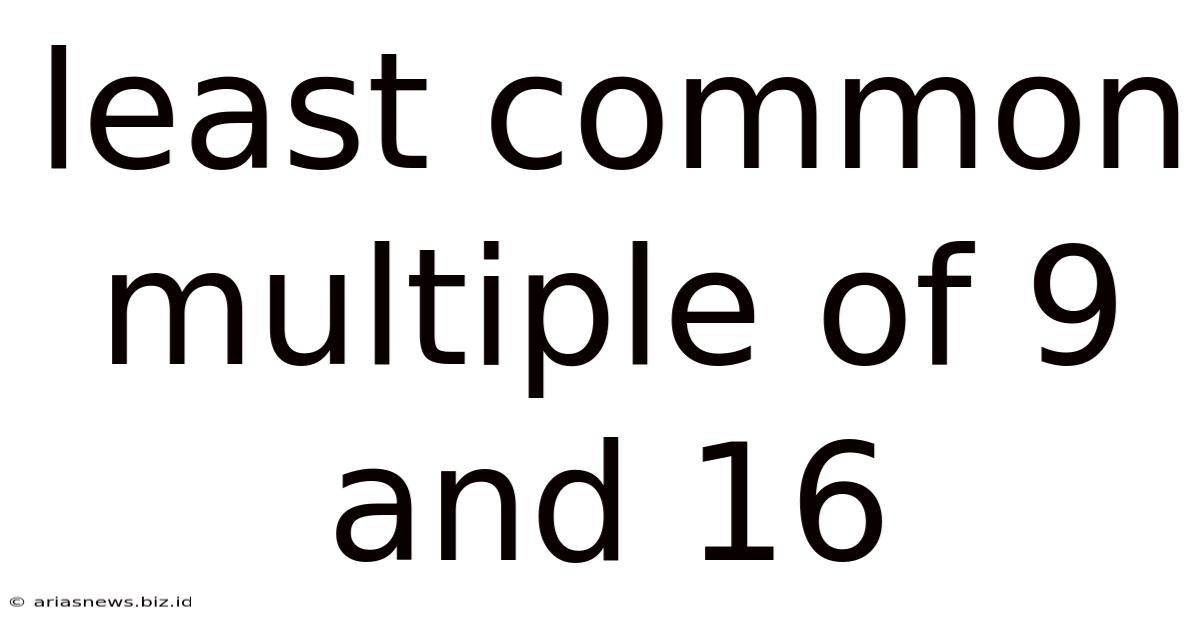
Table of Contents
Finding the Least Common Multiple (LCM) of 9 and 16: A Comprehensive Guide
The least common multiple (LCM) is a fundamental concept in number theory with wide-ranging applications in mathematics, computer science, and various other fields. Understanding how to calculate the LCM is crucial for solving problems related to fractions, scheduling, and rhythmic patterns. This article delves deep into the process of finding the LCM of 9 and 16, exploring various methods and providing a solid foundation for tackling similar problems.
Understanding Least Common Multiple (LCM)
Before we jump into calculating the LCM of 9 and 16, let's clarify the definition. The least common multiple of two or more integers is the smallest positive integer that is divisible by all the integers without leaving a remainder. For example, the LCM of 2 and 3 is 6 because 6 is the smallest positive integer divisible by both 2 and 3.
Key Characteristics of LCM:
- Positive Integer: The LCM is always a positive integer.
- Divisibility: The LCM is divisible by all the numbers involved.
- Smallest Value: It's the smallest positive integer satisfying the divisibility condition.
Methods for Calculating LCM(9, 16)
Several methods exist for computing the LCM of two numbers. We'll explore the most common and effective ones, applying them to find the LCM of 9 and 16.
Method 1: Listing Multiples
This is a straightforward method, especially for smaller numbers. We list the multiples of each number until we find the smallest common multiple.
Multiples of 9: 9, 18, 27, 36, 45, 54, 63, 72, 81, 90, 99, 108, 117, 126, 135, 144...
Multiples of 16: 16, 32, 48, 64, 80, 96, 112, 128, 144, 160...
By comparing the lists, we observe that the smallest common multiple is 144. Therefore, LCM(9, 16) = 144.
This method becomes less efficient with larger numbers, as the lists of multiples can grow significantly.
Method 2: Prime Factorization
This is a more efficient method, especially for larger numbers. It involves finding the prime factorization of each number and then constructing the LCM using the highest powers of all prime factors present.
Prime Factorization of 9: 9 = 3²
Prime Factorization of 16: 16 = 2⁴
To find the LCM, we take the highest power of each prime factor present in the factorizations:
- Highest power of 2: 2⁴ = 16
- Highest power of 3: 3² = 9
LCM(9, 16) = 2⁴ * 3² = 16 * 9 = 144
This method is generally more efficient and less prone to errors than listing multiples, particularly when dealing with larger numbers or more than two numbers.
Method 3: Using the Formula LCM(a, b) = (|a * b|) / GCD(a, b)
This method leverages the relationship between the LCM and the greatest common divisor (GCD) of two numbers. The formula states that the LCM of two numbers (a and b) is equal to the absolute value of their product divided by their greatest common divisor.
First, we need to find the GCD of 9 and 16. The GCD is the largest number that divides both 9 and 16 without leaving a remainder. In this case, the GCD(9, 16) = 1, as 9 and 16 share no common factors other than 1.
Now, we can apply the formula:
LCM(9, 16) = (|9 * 16|) / GCD(9, 16) = (144) / 1 = 144
This method requires knowing how to find the GCD, which can be done using the Euclidean algorithm or prime factorization.
Applications of LCM
The concept of the least common multiple has various applications in diverse fields:
1. Fractions: Finding a Common Denominator
When adding or subtracting fractions with different denominators, finding the LCM of the denominators is crucial for finding a common denominator. This simplifies the addition or subtraction process. For instance, to add 1/9 and 1/16, we would use the LCM (144) as the common denominator.
2. Scheduling and Timing Problems
LCM is frequently used in scheduling problems. For example, imagine two buses arrive at a bus stop at different intervals. Bus A arrives every 9 minutes, while Bus B arrives every 16 minutes. The LCM (144) indicates that both buses will arrive at the bus stop simultaneously after 144 minutes (2 hours and 24 minutes).
3. Cyclic Patterns and Rhythms
LCM finds applications in understanding and predicting cyclical patterns or rhythms. For example, in music, the LCM helps determine when different musical phrases will coincide. In other scenarios involving repeating cycles (like gear rotations or signal frequencies), the LCM is used to predict synchronization points.
4. Modular Arithmetic and Cryptography
LCM plays a significant role in modular arithmetic, which forms the foundation for many cryptographic techniques. Understanding the LCM is essential for working with congruences and solving various problems in this field.
Conclusion
Finding the least common multiple of 9 and 16, whether through listing multiples, prime factorization, or using the LCM/GCD formula, consistently yields the result of 144. This seemingly simple calculation has vast applications across various mathematical disciplines and practical situations. Understanding LCM enhances problem-solving capabilities in diverse fields and underscores the importance of foundational mathematical concepts in a wide array of applications. Mastering LCM calculations is a valuable skill for anyone pursuing studies or careers in mathematics, computer science, engineering, or any field involving quantitative reasoning. The ability to efficiently calculate LCMs empowers individuals to tackle more complex problems and contributes to a stronger analytical foundation.
Latest Posts
Latest Posts
-
How Many Minutes Are In Six Months
May 10, 2025
-
Which Is The Best Example Of A Rhetorical Device
May 10, 2025
-
How Do You Say Hammer In Spanish
May 10, 2025
-
What Do Rfc 349 And Rfc 1700 Have In Common
May 10, 2025
-
Everytime A Bell Rings An Angel Gets Its Wings
May 10, 2025
Related Post
Thank you for visiting our website which covers about Least Common Multiple Of 9 And 16 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.