Lowest Common Factor Of 24 And 30
Arias News
Apr 01, 2025 · 5 min read
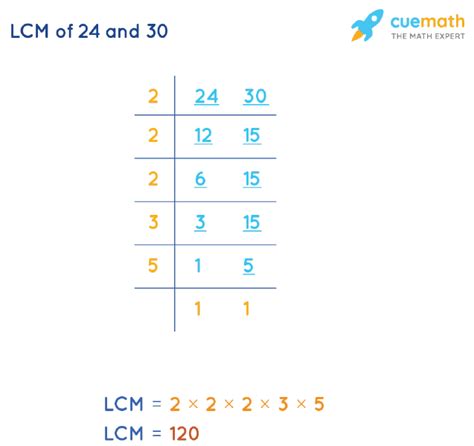
Table of Contents
Finding the Lowest Common Factor (LCF) of 24 and 30: A Comprehensive Guide
The concept of the Lowest Common Factor (LCF), sometimes referred to as the Least Common Multiple (LCM), is a fundamental element in number theory and has wide-ranging applications in various fields, including mathematics, computer science, and engineering. This article will provide a comprehensive guide to understanding and calculating the LCF of 24 and 30, exploring different methods and their underlying principles. We'll delve into the theoretical underpinnings, offer practical examples, and showcase the significance of this concept within a broader mathematical context.
Understanding the Lowest Common Multiple (LCM)
Before we dive into calculating the LCF of 24 and 30, let's clarify the terminology. While some sources might use "Lowest Common Factor," the more standard and widely accepted term is Lowest Common Multiple (LCM). The LCM of two or more integers is the smallest positive integer that is divisible by all the integers. In simpler terms, it's the smallest number that all the given numbers can divide into evenly without leaving a remainder.
Distinguishing LCM from GCF (Greatest Common Factor)
It's crucial to differentiate the LCM from the Greatest Common Factor (GCF), also known as the Greatest Common Divisor (GCD). The GCF is the largest positive integer that divides each of the given integers without leaving a remainder. For example, the GCF of 24 and 30 is 6, as 6 is the largest number that divides both 24 and 30 perfectly. Conversely, the LCM, which we're focusing on here, is the smallest number that both 24 and 30 divide into without a remainder.
Methods for Calculating the LCM of 24 and 30
Several methods exist for calculating the LCM of two numbers. We'll explore three common and effective approaches:
1. Listing Multiples Method
This is a straightforward method, particularly useful for smaller numbers. We list the multiples of each number until we find the smallest multiple common to both.
- Multiples of 24: 24, 48, 72, 96, 120, 144, 168, 192, 216, 240...
- Multiples of 30: 30, 60, 90, 120, 150, 180, 210, 240...
Observing the lists, we see that the smallest multiple common to both 24 and 30 is 120. Therefore, the LCM of 24 and 30 is 120.
This method is simple to understand but can become cumbersome when dealing with larger numbers.
2. Prime Factorization Method
This method is more efficient for larger numbers. It involves finding the prime factorization of each number and then constructing the LCM using the highest powers of each prime factor present.
- Prime factorization of 24: 2³ x 3
- Prime factorization of 30: 2 x 3 x 5
To find the LCM, we take the highest power of each prime factor present in either factorization:
- Highest power of 2: 2³ = 8
- Highest power of 3: 3¹ = 3
- Highest power of 5: 5¹ = 5
Now, multiply these highest powers together: 8 x 3 x 5 = 120. Therefore, the LCM of 24 and 30 is 120.
This method is more systematic and efficient than the listing multiples method, especially for larger numbers.
3. Using the Formula: LCM(a, b) = (|a x b|) / GCF(a, b)
This formula provides a direct way to calculate the LCM using the GCF. We already know the GCF of 24 and 30 is 6. Applying the formula:
LCM(24, 30) = (|24 x 30|) / GCF(24, 30) = (720) / 6 = 120
This method is concise and efficient once you've determined the GCF. Finding the GCF itself can be done using the Euclidean algorithm or prime factorization.
Applications of LCM
The concept of LCM has numerous applications across various fields:
1. Scheduling Problems
Imagine two buses departing from the same station at different intervals. One bus departs every 24 minutes, and the other every 30 minutes. To find when both buses will depart simultaneously again, we need to find the LCM of 24 and 30, which is 120 minutes (or 2 hours).
2. Fraction Operations
When adding or subtracting fractions with different denominators, finding the LCM of the denominators helps determine the least common denominator (LCD), simplifying the calculation process.
3. Gear Ratios and Mechanical Engineering
In mechanical systems involving gears, the LCM plays a crucial role in determining the synchronization of rotating components. Understanding gear ratios relies heavily on the LCM to ensure smooth and efficient operation.
4. Computer Science and Algorithms
LCM calculations are often integrated into algorithms dealing with cyclic events, scheduling tasks, and optimizing resource allocation in computer systems.
5. Music Theory
The LCM is utilized in music theory to determine the least common period of rhythmic patterns or when different musical phrases will coincide again.
Advanced Concepts Related to LCM
The concepts of LCM extend beyond simple integer calculations. We can find the LCM of more than two numbers by extending the prime factorization method or applying the formula iteratively. Furthermore, the concept of LCM can be extended to other algebraic structures beyond integers.
Conclusion
The LCM of 24 and 30 is 120. We've explored three effective methods for determining this: the listing multiples method, the prime factorization method, and the formula utilizing the GCF. Understanding the LCM is essential not only for mathematical proficiency but also for solving real-world problems across various disciplines. This comprehensive guide aims to solidify your grasp of this fundamental concept and its diverse applications, empowering you to tackle more complex mathematical challenges. The methods outlined provide a robust foundation for calculating LCMs, regardless of the size or complexity of the numbers involved. Remember that choosing the most efficient method depends on the specific context and the numbers you're working with. Practice with different examples to further strengthen your understanding and skills in this important area of mathematics.
Latest Posts
Latest Posts
-
What Does Tk316 Mean On A Ring
Apr 02, 2025
-
Least Common Multiple Of 18 And 21
Apr 02, 2025
-
How Tall Is 23 Inches In Feet
Apr 02, 2025
-
How Much Is 95 Ounces Of Water
Apr 02, 2025
-
Which Element Must An Effective Wartime Speech Have
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about Lowest Common Factor Of 24 And 30 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
