Negative Two-thirds Times A Number Is At Least 12.
Arias News
May 09, 2025 · 5 min read
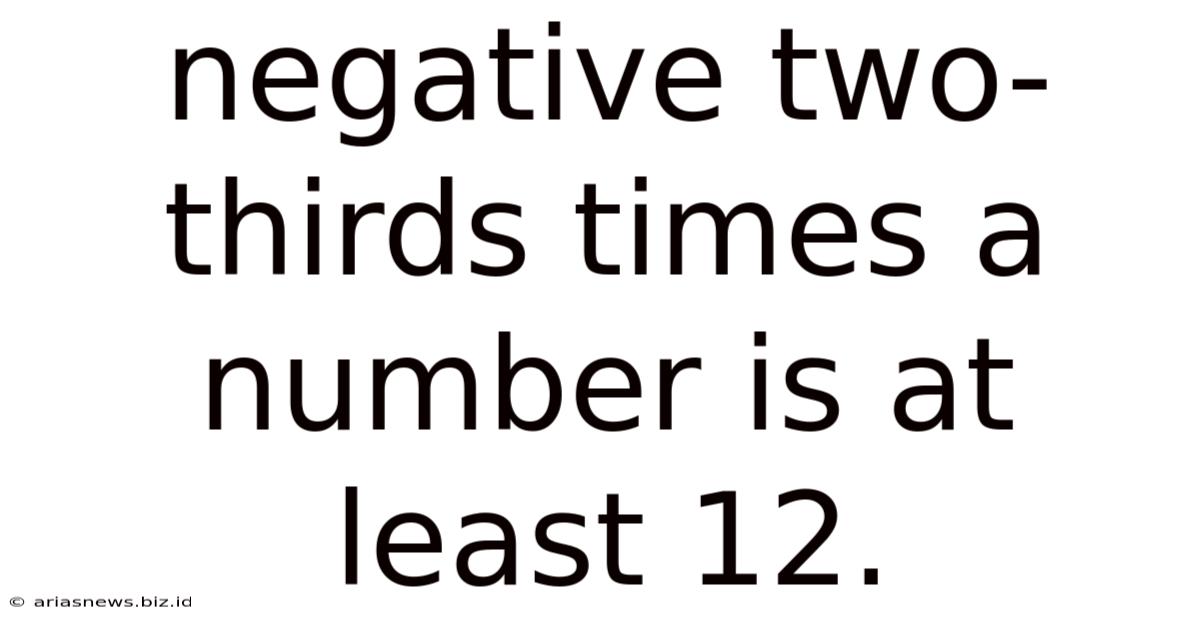
Table of Contents
Negative Two-Thirds Times a Number is at Least 12: A Deep Dive into Inequalities
This article explores the mathematical inequality "-⅔x ≥ 12," breaking down its solution, practical applications, and related concepts. We will delve into the intricacies of solving inequalities, emphasizing the importance of understanding the underlying principles and their real-world implications. We'll also touch upon related concepts to provide a comprehensive understanding of this type of problem.
Understanding the Inequality: -⅔x ≥ 12
The inequality "-⅔x ≥ 12" states that negative two-thirds of a number (represented by 'x') is greater than or equal to 12. This seemingly simple statement opens the door to a world of mathematical exploration and problem-solving techniques. Let's dissect it step-by-step.
Key Components:
- -⅔: This is the coefficient of 'x,' representing a negative fraction. Understanding the implications of a negative coefficient is crucial for correctly solving the inequality.
- x: This is the variable, representing the unknown number we aim to find.
- ≥: This symbol denotes "greater than or equal to." This means the solution includes values of 'x' that make the left side equal to 12, as well as values that make it greater than 12.
- 12: This is the constant on the right side of the inequality, representing the lower bound of the solution.
Solving the Inequality: A Step-by-Step Guide
Solving inequalities involves manipulating the equation to isolate the variable. However, unlike equations, manipulating inequalities requires careful attention to the direction of the inequality sign.
Step 1: Multiply Both Sides by -3/2
To isolate 'x', we need to multiply both sides of the inequality by the reciprocal of -⅔, which is -³/₂. Crucially, because we're multiplying by a negative number, we must reverse the direction of the inequality sign.
(-³/₂)(-⅔x) ≥ (-³/₂)(12)
This simplifies to:
x ≤ -18
Step 2: Understanding the Solution
The solution, x ≤ -18, means that any number less than or equal to -18 will satisfy the original inequality. This represents an infinite set of numbers.
Step 3: Verification
Let's test a few values to verify our solution:
- x = -18: (-⅔)(-18) = 12. This satisfies the inequality (12 ≥ 12).
- x = -20: (-⅔)(-20) = 40/3 ≈ 13.33. This also satisfies the inequality (13.33 ≥ 12).
- x = -10: (-⅔)(-10) = 20/3 ≈ 6.67. This does not satisfy the inequality (6.67 ≱ 12).
These tests confirm that our solution, x ≤ -18, is correct.
Graphical Representation of the Solution
The solution x ≤ -18 can be visually represented on a number line. We would place a closed circle (or a filled-in dot) at -18 to indicate that -18 is included in the solution set, and then shade the number line to the left of -18, signifying all numbers less than -18 are also part of the solution.
(Insert image of a number line with a closed circle at -18 and shading to the left)
Real-World Applications of Inequalities
Inequalities are far more than abstract mathematical concepts; they have widespread applications in various fields. Here are a few examples demonstrating the practicality of solving inequalities like "-⅔x ≥ 12":
1. Budgeting and Finance:
Imagine you're managing a budget, and you need to ensure your expenses are at least two-thirds of your income. If your income is represented by 'x', and you need to spend at least 12 units of currency, the inequality would help you determine the minimum income required.
2. Engineering and Physics:
Inequalities are frequently used in engineering and physics to determine safety margins, tolerances, and constraints. For example, in structural engineering, the stress on a component must be less than a critical value to prevent failure.
3. Environmental Science:
Inequalities can model environmental thresholds. For instance, a certain pollutant concentration in water must not exceed a specific limit. The inequality could be used to determine the maximum allowable emissions.
4. Business and Economics:
In business, inequalities can be used to model profit margins, production limits, and market share. Understanding the minimum sales needed to meet certain targets is a common use case.
Further Exploration: Related Mathematical Concepts
Understanding "-⅔x ≥ 12" allows us to explore other relevant mathematical concepts:
1. Absolute Value Inequalities:
Absolute value inequalities involve expressions containing the absolute value operator (| |). Solving these requires considering both positive and negative cases. For example, |x| ≥ 5 means x ≥ 5 or x ≤ -5.
2. Compound Inequalities:
Compound inequalities involve combining two or more inequalities using "and" or "or." For example, x > 2 and x < 10. Solving compound inequalities requires finding the intersection or union of the solution sets for individual inequalities.
3. Linear Programming:
Linear programming uses inequalities (and equalities) to model optimization problems. These problems involve finding the best possible solution (e.g., maximizing profit or minimizing cost) under given constraints.
4. Set Theory:
The solution to the inequality -⅔x ≥ 12, x ≤ -18, can be expressed using set notation as {x | x ∈ ℝ, x ≤ -18}, which reads as "the set of all x such that x is a real number and x is less than or equal to -18."
Conclusion: Mastering Inequalities for a Broader Mathematical Understanding
Solving inequalities like "-⅔x ≥ 12" provides a fundamental understanding of algebraic manipulation and its practical applications across diverse fields. The ability to translate real-world problems into mathematical inequalities is a crucial skill for anyone pursuing studies or careers in STEM fields, economics, business, or related areas. Mastering these techniques empowers us to analyze, solve, and interpret a wide array of complex situations. Remember the key steps: isolate the variable, carefully consider the effect of multiplying or dividing by negative numbers, and always verify your solution. The journey to understanding inequalities is a rewarding one, paving the way for greater proficiency in mathematics and its myriad applications.
Latest Posts
Latest Posts
-
What Does Que Linda Mean In Spanish
May 10, 2025
-
8 Oz Of Cream Cheese Is How Many Grams
May 10, 2025
-
Can Banks Be Closed Three Days In A Row
May 10, 2025
-
Distance From Chandler Az To Phoenix Az
May 10, 2025
-
How Fast Is 22 Km Per Hour
May 10, 2025
Related Post
Thank you for visiting our website which covers about Negative Two-thirds Times A Number Is At Least 12. . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.