Square And Square Toot The Same Answer
Arias News
Apr 07, 2025 · 6 min read
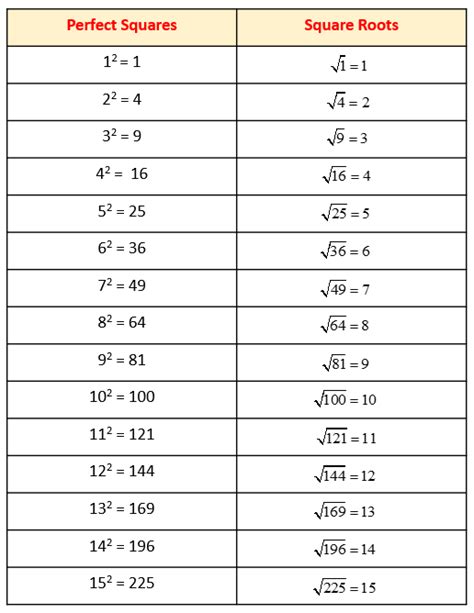
Table of Contents
Squares and Square Roots: Exploring the Intimate Relationship Between Inverses
Squares and square roots, while seemingly distinct mathematical concepts, are intrinsically linked as inverse operations. Understanding this fundamental relationship is crucial for grasping various mathematical principles and applications across different fields. This comprehensive exploration delves into the definitions, properties, and applications of squares and square roots, highlighting their interconnectedness and demonstrating how they work in harmony.
Understanding Squares: The Foundation
A square, in the mathematical sense, is the result of multiplying a number by itself. This is often represented as x², where x represents the number being squared (also called the base). The operation of squaring a number is a fundamental aspect of algebra and arithmetic.
Properties of Squares:
- Always Positive (or Zero): Regardless of whether the base (x) is positive or negative, the square (x²) will always be non-negative (positive or zero). This is because the product of two negative numbers is a positive number. For example, (-3)² = (-3) * (-3) = 9.
- Even Numbers Squared: When an even number is squared, the result is always an even number. This is because an even number can be expressed as 2k (where k is an integer), and (2k)² = 4k², which is divisible by 4 and hence even.
- Odd Numbers Squared: Similarly, when an odd number is squared, the result is always an odd number. An odd number can be expressed as 2k + 1, and (2k + 1)² = 4k² + 4k + 1, which leaves a remainder of 1 when divided by 2, thus being odd.
- Perfect Squares: Certain numbers are known as perfect squares because they are the squares of integers. For instance, 9 (3²), 16 (4²), and 25 (5²) are perfect squares. Identifying perfect squares is often helpful in simplifying calculations and solving equations.
- Geometric Interpretation: The concept of a square has a strong geometric connection. The area of a square with side length x is precisely x². This visual representation helps solidify the understanding of squaring.
Unveiling Square Roots: The Inverse Operation
A square root is the inverse operation of squaring. It's the number that, when multiplied by itself, gives the original number. The square root of x is denoted as √x. Finding the square root is essentially asking, "What number, when squared, equals x?"
Properties of Square Roots:
- Principal Square Root: Every positive number has two square roots: one positive and one negative. However, the principal square root is conventionally defined as the non-negative square root. For example, the square roots of 9 are 3 and -3, but the principal square root of 9 is 3.
- Square Root of Zero: The square root of 0 is 0 (√0 = 0).
- Square Root of Negative Numbers: The square root of a negative number is not a real number. It involves the concept of imaginary numbers, denoted with the imaginary unit i, where i² = -1. For instance, √(-9) = 3i.
- Simplifying Square Roots: Square roots can often be simplified by factoring. For example, √12 can be simplified to 2√3 because 12 = 4 * 3, and √4 = 2.
- Geometric Interpretation: Geometrically, finding the square root of an area corresponds to finding the side length of a square with that area.
The Intimate Relationship: Squares and Square Roots as Inverses
The core relationship between squares and square roots lies in their inverse nature. This means that they "undo" each other. Specifically:
- √(x²) = |x|: The square root of a number squared is the absolute value of that number. This is because squaring removes the sign, and the square root operation returns only the positive (principal) root.
- (√x)² = x (for x ≥ 0): Squaring the square root of a non-negative number returns the original number.
This inverse relationship is fundamental in solving equations. For example, to solve the equation x² = 25, we take the square root of both sides, resulting in x = ±5. This demonstrates the practical application of the inverse relationship in finding solutions.
Applications Across Disciplines
The concepts of squares and square roots have far-reaching applications in various fields:
Mathematics:
- Solving Quadratic Equations: Quadratic equations, which have the form ax² + bx + c = 0, are solved using the quadratic formula, which involves square roots.
- Geometry and Trigonometry: Calculating areas, volumes, distances, and angles often involves squares and square roots. The Pythagorean theorem (a² + b² = c²) is a prime example of this application.
- Calculus: Derivatives and integrals frequently involve the manipulation of square roots and squares.
- Number Theory: Concepts like perfect squares and the study of square-free integers are significant in number theory.
Physics and Engineering:
- Kinematics: Calculating velocity, acceleration, and displacement often involves the use of square roots and squares.
- Mechanics: Many physical formulas, such as those related to energy, momentum, and force, incorporate squares and square roots.
- Electrical Engineering: Calculating impedance, power, and other electrical quantities relies on these operations.
Computer Science:
- Graphics and Image Processing: Calculations involving coordinates, distances, and transformations frequently utilize squares and square roots.
- Algorithms and Data Structures: Certain algorithms, such as those for searching and sorting, benefit from utilizing properties of squares and square roots for efficiency.
- Cryptography: Square roots and squares play roles in several cryptographic algorithms.
Finance and Statistics:
- Financial Modeling: Square roots are used in various financial calculations, such as standard deviation and variance.
- Statistical Analysis: Many statistical formulas employ squares and square roots in the calculation of measures of variability and dispersion.
Advanced Concepts and Extensions
Beyond the basics, the concepts of squares and square roots extend to more advanced areas:
- Higher-Order Roots: The concept generalizes beyond square roots to cube roots (∛x), fourth roots (⁴√x), and so on, representing the inverse operation of raising a number to the corresponding power.
- Complex Numbers: As mentioned earlier, square roots of negative numbers lead to complex numbers, expanding the number system beyond real numbers.
- Matrices and Linear Algebra: The concept of squaring extends to matrices, where matrix multiplication is used to obtain the square of a matrix. The concept of eigenvalues and eigenvectors is also closely related.
Conclusion: A Fundamental Partnership
Squares and square roots represent a fundamental partnership in mathematics. Their inverse relationship simplifies complex calculations and provides solutions to numerous problems across various disciplines. By understanding their properties, applications, and interconnectedness, one can enhance their mathematical proficiency and appreciate their profound impact on various fields of study and real-world applications. Their seemingly simple nature belies a depth of mathematical richness that continues to influence our understanding of the world around us. Further exploration into these concepts will inevitably unveil more fascinating insights into their power and utility.
Latest Posts
Latest Posts
-
What Year Was I Born If Im 61
Apr 08, 2025
-
How Much Is 96 Oz In Gallons
Apr 08, 2025
-
Which Sentence Most Accurately Describes A Feature Of Elizabethan Drama
Apr 08, 2025
-
How Big Is An Acre In Yards
Apr 08, 2025
-
Average Height Of An 8 Year Old Boy
Apr 08, 2025
Related Post
Thank you for visiting our website which covers about Square And Square Toot The Same Answer . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.