Square Root Of 3 Divided By 2
Arias News
May 08, 2025 · 5 min read
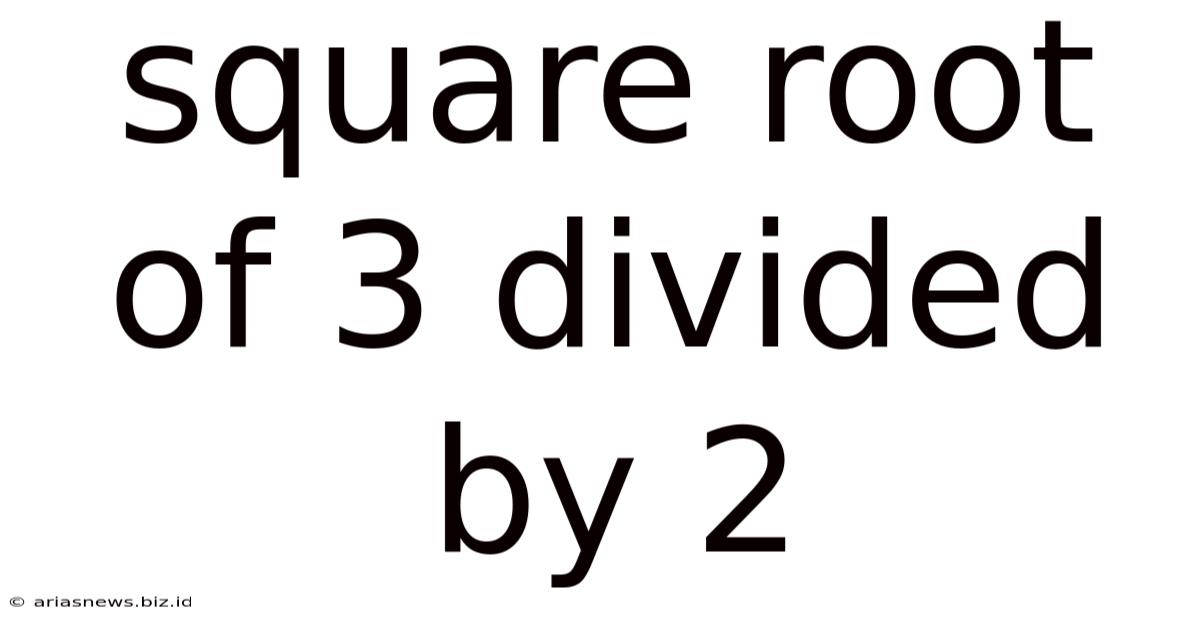
Table of Contents
Decoding the Mathematical Mystery: Exploring √3/2
The seemingly simple expression, √3/2, hides a wealth of mathematical significance and practical applications. Far from being just a dry algebraic term, this fraction represents a cornerstone in trigonometry, geometry, and even physics. This comprehensive exploration will delve into its properties, derivations, applications, and the intriguing connections it holds within the broader mathematical landscape.
Understanding the Fundamentals: What Does √3/2 Represent?
At its core, √3/2 represents a specific ratio – the ratio of the length of the shorter side to the hypotenuse of a 30-60-90 triangle. This special right-angled triangle forms the basis for many geometrical calculations and trigonometric identities. The value of √3/2 is approximately 0.866, a recurring decimal that continues infinitely. Its importance stems not from its numerical value alone, but from its recurring appearance in various mathematical contexts. Understanding this ratio allows for efficient calculation and problem-solving across multiple mathematical disciplines.
The 30-60-90 Triangle: The Geometric Heart of √3/2
The 30-60-90 triangle is a fundamental geometrical construct. Its angles, in degrees, are 30, 60, and 90. The sides of this triangle exhibit a specific ratio, often expressed in terms of a variable, x:
- Opposite to 30°: x
- Opposite to 60°: x√3
- Opposite to 90° (Hypotenuse): 2x
This ratio directly leads to the derivation of √3/2. If we consider the sine of 60°, we get:
sin(60°) = (Opposite side) / (Hypotenuse) = (x√3) / (2x) = √3/2
Similarly, the cosine of 30° yields the same result:
cos(30°) = (Adjacent side) / (Hypotenuse) = (x√3) / (2x) = √3/2
This highlights the intrinsic link between the 30-60-90 triangle and the value √3/2.
Trigonometric Connections: Sine, Cosine, and Beyond
The relationship between √3/2 and trigonometric functions extends beyond the 30-60-90 triangle. It plays a crucial role in understanding and calculating values for various angles.
Sine and Cosine of Key Angles
The value of √3/2 is precisely the sine of 60° and the cosine of 30°. This fact is instrumental in simplifying trigonometric expressions and solving trigonometric equations. Understanding this foundational relationship unlocks a deeper understanding of trigonometric identities and their applications.
Application in Unit Circle
The unit circle, a circle with a radius of 1 centered at the origin of a coordinate plane, serves as a visual representation of trigonometric functions. The coordinates of points on the unit circle are directly related to sine and cosine values. The points corresponding to angles of 30° and 60° inherently involve the value √3/2, reinforcing its importance within this critical geometrical construct.
Trigonometric Identities and Simplification
Numerous trigonometric identities involve the value √3/2. This allows for simplification of complex expressions, leading to more concise and manageable solutions. The ability to recognize and utilize this constant within trigonometric identities is a cornerstone of effective trigonometric problem-solving.
Applications Across Disciplines: Geometry, Physics, and Engineering
The mathematical significance of √3/2 extends far beyond theoretical calculations. Its practical applications are widespread across various fields.
Geometry and Spatial Reasoning
In geometry, √3/2 appears frequently in calculations involving regular polygons, particularly hexagons and equilateral triangles. Understanding this value streamlines the process of calculating areas, perimeters, and other geometrical properties of these shapes.
Physics: Vectors and Forces
In physics, the value √3/2 appears when resolving vectors into their components. This is especially relevant in situations involving forces acting at angles, such as inclined plane problems or projectile motion calculations. The value aids in efficient determination of force components along different axes.
Engineering and Design: Structural Analysis
In structural engineering, understanding the relationships within triangles is crucial for stability calculations. The 30-60-90 triangle and its inherent ratio, √3/2, become relevant in design considerations for structures that rely on triangular supports.
Computer Graphics and Game Development
The value also finds its place in computer graphics and game development. The precise rendering of 3D objects often involves calculations that directly leverage the trigonometric properties related to √3/2, ensuring realistic and accurate visual representations.
Further Exploration: Advanced Mathematical Connections
The mathematical implications of √3/2 extend beyond the realms mentioned above. It intertwines with more advanced mathematical concepts.
Complex Numbers
The value is related to complex numbers, appearing in expressions involving Euler's formula (e^(ix) = cos(x) + i sin(x)). This connection strengthens its significance within the broader mathematical framework.
Calculus and Series Expansions
√3/2 can be incorporated into Taylor and Maclaurin series expansions of trigonometric functions, demonstrating its use in advanced calculus calculations. These expansions further emphasize its importance in approximating trigonometric function values.
Group Theory and Symmetry
Its role in describing geometrical symmetry and transformations in group theory enhances its mathematical importance. Understanding its connection within group theory provides a deeper understanding of symmetry operations and their mathematical representation.
Conclusion: The Enduring Importance of √3/2
√3/2, while seemingly a simple fraction, stands as a significant constant within mathematics and its applications. Its deep connection to trigonometry, geometry, physics, and engineering makes it an indispensable value for students and professionals alike. Beyond its numerical value, the significance lies in its inherent ability to streamline calculations, simplify complex expressions, and offer elegant solutions in various scenarios. Its recurring presence underscores its enduring importance within the broader mathematical landscape. Understanding this constant unlocks a deeper appreciation for the interconnectedness of mathematical concepts and their practical applications in the real world. Further exploration into its applications can reveal even more profound connections within mathematics and its various branches, underscoring its enduring relevance in the field.
Latest Posts
Latest Posts
-
How Do You Say Hi In Navajo
May 08, 2025
-
What Does Phi Phi Mean In Pike
May 08, 2025
-
How Much Do Repo Guys Make Per Car
May 08, 2025
-
Words To Describe Veterans That Start With E
May 08, 2025
-
How Much Does 40 Pack Of Water Weigh
May 08, 2025
Related Post
Thank you for visiting our website which covers about Square Root Of 3 Divided By 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.