The Sum Of A Number And 8
Arias News
May 12, 2025 · 6 min read
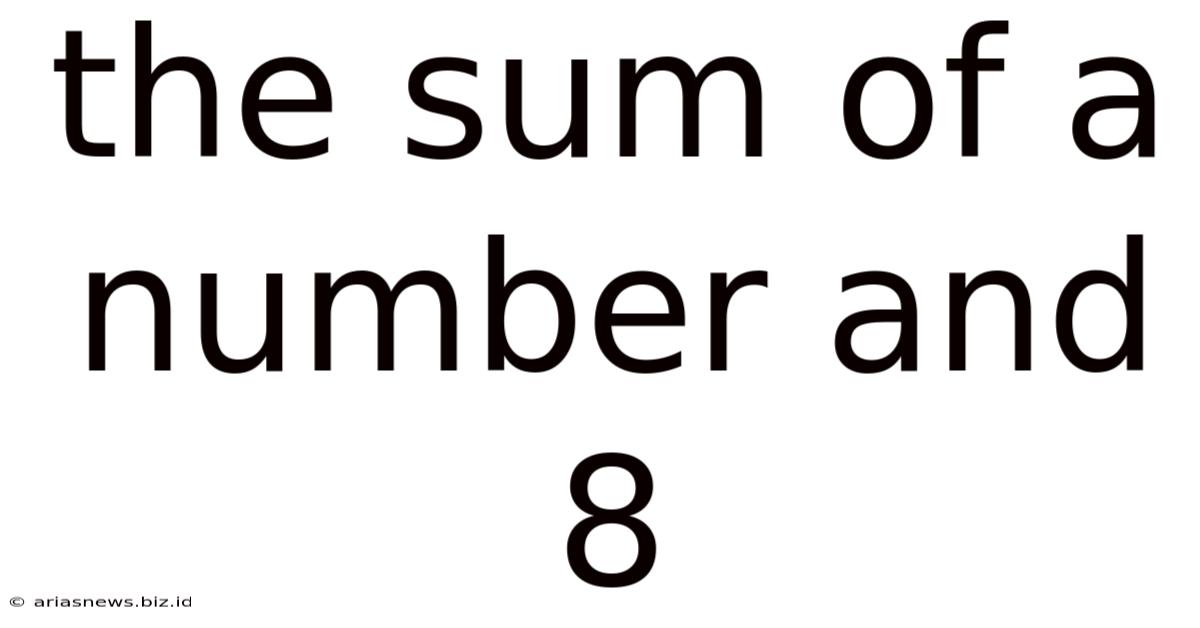
Table of Contents
The Sum of a Number and 8: A Deep Dive into Mathematical Concepts and Applications
The seemingly simple expression "the sum of a number and 8" opens a door to a wide range of mathematical concepts and practical applications. While the immediate understanding is straightforward – adding 8 to an unknown number – delving deeper reveals its significance in algebra, number theory, and even everyday problem-solving. This article will explore this seemingly simple expression, examining its implications in various mathematical contexts and showcasing its practical use in real-world scenarios.
Understanding the Fundamentals: Variables and Equations
At its core, "the sum of a number and 8" represents an algebraic expression. The "number" is an unknown value, typically represented by a variable, often x. Therefore, the expression translates to the algebraic equation: x + 8. This simple equation forms the bedrock of more complex algebraic manipulations.
The Power of Variables
The use of a variable (x) is crucial. It allows us to generalize the concept. We're not limited to a specific number; x can represent any real number – positive, negative, integer, fraction, or irrational. This ability to represent an unknown quantity is fundamental to algebra and its ability to solve a vast range of problems.
Solving for x: Finding the Unknown
While x + 8 is an expression, it becomes an equation when we set it equal to another value. For instance:
- x + 8 = 15
This equation asks: "What number, when added to 8, equals 15?" Solving this involves basic algebra: subtracting 8 from both sides to isolate x. The solution is x = 7.
This seemingly simple process demonstrates the power of algebraic manipulation. The same process can be applied to any equation of the form x + 8 = y, where y represents any known value. This allows us to find the unknown number (x) given the sum (y).
Exploring Different Number Systems
The expression "x + 8" can be explored within different number systems, each with its own unique properties.
Integers: The Whole Numbers and Their Opposites
Within the system of integers (…-3, -2, -1, 0, 1, 2, 3…), adding 8 to any integer results in another integer. For example:
- -5 + 8 = 3
- 0 + 8 = 8
- 12 + 8 = 20
The operation remains consistent and straightforward, maintaining the integrity of the integer number system.
Real Numbers: Expanding the Possibilities
When we consider the real number system (including all rational and irrational numbers), the possibilities expand significantly. Adding 8 to a real number, such as π (pi) or √2 (the square root of 2), results in another real number:
- π + 8 ≈ 11.1416
- √2 + 8 ≈ 9.4142
The operation remains well-defined, even with irrational numbers, preserving the completeness of the real number system.
Complex Numbers: Stepping into a Higher Dimension
Even in the realm of complex numbers (numbers of the form a + bi, where 'a' and 'b' are real numbers and 'i' is the imaginary unit, √-1), the concept holds true. Adding 8 to a complex number results in another complex number:
- (3 + 2i) + 8 = 11 + 2i
The real part (3) and the imaginary part (2i) are simply added to 8, demonstrating the extension of the operation to a higher-dimensional number system.
Applications in Real-World Scenarios
The seemingly simple "x + 8" has far-reaching practical applications.
Everyday Arithmetic: Budgeting, Shopping, and More
In everyday life, adding 8 (or any number) to another frequently occurs. For example:
- Budgeting: If you have $x in your account and spend $8, the remaining balance can be represented as x - 8. Conversely, if you deposit $8, your new balance is x + 8.
- Shopping: If a product costs $x and you add 8% sales tax, the total cost is x + 0.08x (or 1.08x). This demonstrates how a simple addition forms the basis of percentage calculations.
- Distance Calculations: If you travel x kilometers and then travel another 8 kilometers, your total distance is x + 8 kilometers.
These examples highlight the frequent and often unnoticed application of simple addition in daily life.
Problem Solving and Word Problems
Word problems often require translating a real-world scenario into an algebraic equation. Consider this example:
"John has some apples (x). His friend gives him 8 more. Now he has 17 apples. How many apples did John have initially?"
This translates to the equation x + 8 = 17, with the solution x = 9. Solving this equation relies on the fundamental understanding of the expression "x + 8".
Advanced Applications: Physics, Engineering, and Computer Science
The concept of adding a constant to a variable is fundamental in many scientific and engineering disciplines.
- Physics: In kinematic equations, displacement might be represented by x + vt + at²/2, where x is the initial position, v is the initial velocity, a is acceleration, and t is time. The initial position (x) functions as a constant added to other terms representing changes in position over time.
- Engineering: In various engineering problems, adding a constant (8, in our example) might represent a fixed factor like a load, resistance, or offset value.
- Computer Science: In programming, adding 8 might involve incrementing a counter, adding a constant offset to a memory address, or performing other basic arithmetic operations.
Expanding the Concept: More Complex Equations and Inequalities
The "x + 8" concept extends beyond simple equations.
Inequalities: Exploring Ranges of Solutions
Instead of an equation, we might have an inequality:
- x + 8 > 15 (x + 8 is greater than 15)
Solving this involves the same subtraction principle, leading to x > 7. This means any number greater than 7 satisfies the inequality.
Similar principles apply to inequalities like x + 8 < 15, x + 8 ≥ 15, and x + 8 ≤ 15, yielding different solution ranges.
Systems of Equations: Solving Multiple Equations Simultaneously
Multiple equations involving "x + 8" or similar expressions can form a system of equations. For instance:
- x + 8 = 15
- x - 3 = 4
Solving this system involves finding the value of x that satisfies both equations. In this case, x = 7 satisfies the first equation but not the second (7-3 ≠ 4). This illustrates that systems of equations can have unique solutions, multiple solutions, or no solution.
Quadratic Equations and Beyond
While not directly related to a simple x + 8, the underlying concept of adding a constant extends to more complex equations like quadratic equations (e.g., x² + 8x + 15 = 0). Solving such equations involves factoring, the quadratic formula, or other techniques, which build upon the fundamental algebraic principles introduced earlier.
Conclusion: The Enduring Significance of a Simple Sum
The seemingly trivial expression "the sum of a number and 8" reveals a surprising depth when explored through the lens of mathematics. From its role in basic algebra to its applications in various scientific and real-world contexts, this simple expression demonstrates the power and versatility of fundamental mathematical concepts. Understanding this expression, and the principles behind it, provides a solid foundation for tackling more complex mathematical challenges and solving problems in diverse fields. The beauty of mathematics lies in its ability to translate seemingly simple concepts into powerful tools for understanding and solving a wide array of problems. This simple sum is a testament to that power.
Latest Posts
Latest Posts
-
How To Address A Letter To A Nursing Home Resident
May 12, 2025
-
Can Bearded Dragons Eat Brussel Sprout Leaves
May 12, 2025
-
How Many Right Angles Does Trapezoid Have
May 12, 2025
-
Kohler 52 50 02 S Cross Reference
May 12, 2025
-
How Much Is 1 Acre Of Land In Mexico
May 12, 2025
Related Post
Thank you for visiting our website which covers about The Sum Of A Number And 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.