Three Less Than Six Times A Number
Arias News
May 10, 2025 · 5 min read
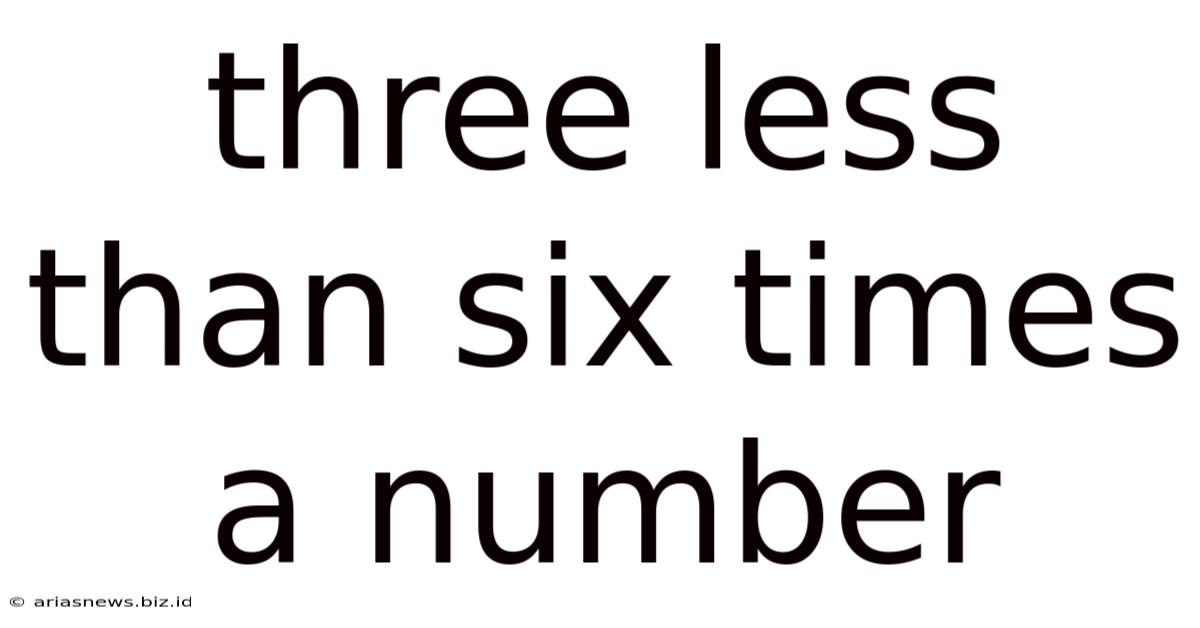
Table of Contents
Three Less Than Six Times a Number: A Deep Dive into Algebraic Expressions
This seemingly simple phrase, "three less than six times a number," opens a door to a vast world of algebraic concepts. Understanding how to translate this phrase into a mathematical expression, solve equations built around it, and apply it to real-world scenarios is crucial for anyone hoping to master algebra. This comprehensive guide will explore these aspects, from the basics to more advanced applications.
Understanding the Phrase: Deconstructing the Problem
Before diving into equations, let's break down the phrase itself: "three less than six times a number."
- A number: This represents an unknown value, which we typically denote with a variable, usually x.
- Six times a number: This translates directly to 6x (or 6x). Multiplication is implied by the word "times."
- Three less than: This signifies subtraction. We're taking three away from the result of "six times a number."
Therefore, the complete algebraic expression for "three less than six times a number" is 6x - 3. It's crucial to understand the order of operations here; subtracting three after multiplying by six is essential to accurately representing the phrase.
Constructing and Solving Equations
Now that we have our algebraic expression, we can use it to create and solve various equations. Let's explore a few examples:
Example 1: Finding the Number
Let's say "three less than six times a number is 21." We can translate this into an equation:
6x - 3 = 21
To solve for x, we follow these steps:
- Add 3 to both sides: 6x = 24
- Divide both sides by 6: x = 4
Therefore, the number is 4.
Example 2: A More Complex Equation
Let's consider a slightly more complex scenario: "Twice the result of three less than six times a number is equal to 30." This translates to:
2(6x - 3) = 30
Solving this equation requires a slightly different approach:
- Distribute the 2: 12x - 6 = 30
- Add 6 to both sides: 12x = 36
- Divide both sides by 12: x = 3
In this case, the number is 3.
Example 3: Equations with Variables on Both Sides
Let's look at a scenario involving variables on both sides of the equation: "Three less than six times a number is equal to five times the number plus six."
This translates to:
6x - 3 = 5x + 6
Solving this involves manipulating the equation to isolate x:
- Subtract 5x from both sides: x - 3 = 6
- Add 3 to both sides: x = 9
Here, the number is 9.
Real-World Applications: Bringing it to Life
While seemingly abstract, algebraic expressions like "three less than six times a number" have numerous practical applications. Let's explore a few:
Scenario 1: Profit Calculation
Imagine a small business owner who sells handmade crafts. They make a profit of six dollars on each item, but they have three dollars in fixed costs per day. The total profit (P) for a day where they sell x crafts can be represented as:
P = 6x - 3
This equation directly mirrors our original phrase. By substituting different values for x (the number of crafts sold), the business owner can quickly calculate their daily profit.
Scenario 2: Geometry Problems
Consider a rectangle where the length is six times the width, minus three units. If the length is represented by l and the width by w, we can write:
l = 6w - 3
Knowing this relationship, we can solve for either the length or the width if we have the value of the other dimension. This demonstrates how the expression applies to geometrical calculations.
Scenario 3: Age-Related Problems
Suppose someone is three years younger than six times their child's age. If the person's age is P and the child's age is C, we have:
P = 6C - 3
This equation allows us to determine one age if the other is known. Many word problems involving age differences can be solved using similar algebraic expressions.
Expanding the Concept: Inequalities and More
The "three less than six times a number" expression isn't limited to equations. It can also be used in inequalities:
Example: Inequality Problem
Let's say "three less than six times a number is greater than 15." This translates to:
6x - 3 > 15
Solving this inequality follows a similar process to solving equations, but with an important distinction: when multiplying or dividing by a negative number, you must reverse the inequality sign.
- Add 3 to both sides: 6x > 18
- Divide both sides by 6: x > 3
This means the number must be greater than 3.
Beyond the Basics: Further Exploration
Understanding "three less than six times a number" lays a foundation for more advanced algebraic concepts:
- Functions: This expression can be readily represented as a function: f(x) = 6x - 3. This allows for exploring concepts like domain, range, and graphing.
- Systems of Equations: Imagine a scenario involving two such expressions; solving them simultaneously introduces the concept of systems of equations, another cornerstone of algebra.
- Quadratic Equations: While not directly related, understanding linear expressions is essential before tackling quadratic equations, which involve squared terms.
Conclusion: Mastering the Fundamentals
The phrase "three less than six times a number," although seemingly simple, encapsulates the fundamental principles of algebra. By understanding how to translate it into mathematical expressions, construct and solve equations, and apply it to real-world problems, you solidify your grasp of core algebraic concepts. This understanding is not only crucial for academic success but also invaluable for solving practical problems across various fields. The journey from simple phrases to complex mathematical models begins with a solid foundation, and this seemingly simple expression is a perfect starting point. Remember to practice regularly, explore different problem types, and don't hesitate to seek help when needed. Mastering algebra is a rewarding endeavor, and understanding even the simplest expressions is a crucial step in that journey.
Latest Posts
Latest Posts
-
What Is A Quarter Of A Cup In Ounces
May 10, 2025
-
What Do Gatsby And Nick Have In Common
May 10, 2025
-
Can You Keep Hot Pockets In The Fridge
May 10, 2025
-
How Do You Say Light In Latin
May 10, 2025
-
What Grade Is 83 Out Of 100
May 10, 2025
Related Post
Thank you for visiting our website which covers about Three Less Than Six Times A Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.