Twice The Sum Of A Number And 5.
Arias News
May 11, 2025 · 5 min read
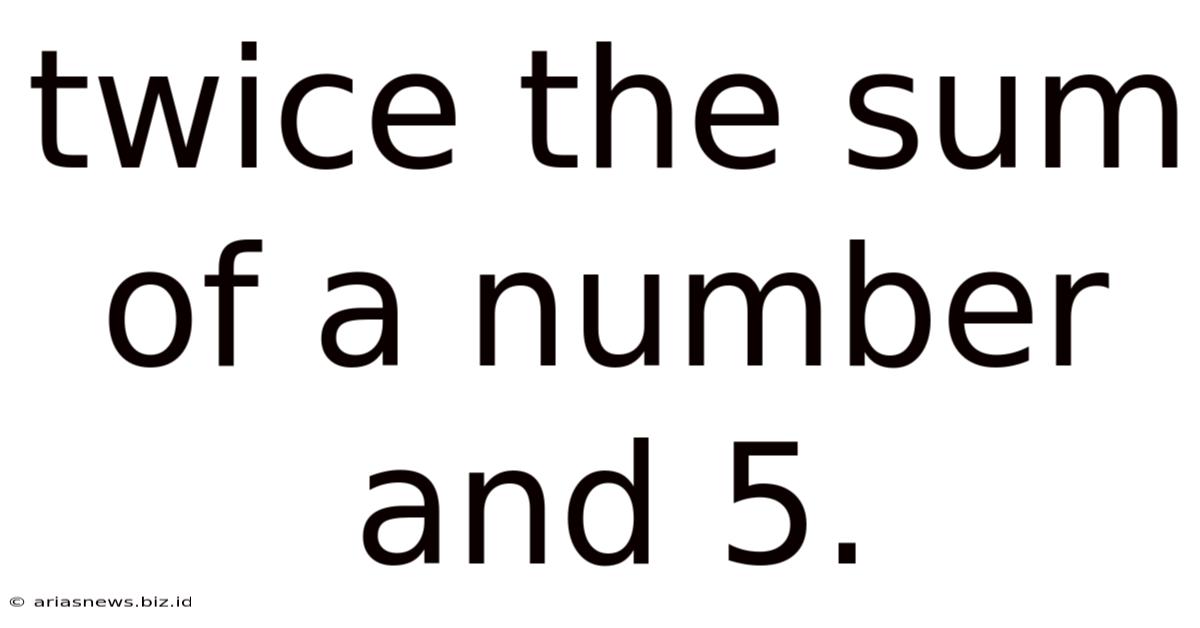
Table of Contents
Twice the Sum of a Number and 5: Exploring Mathematical Concepts and Real-World Applications
This seemingly simple phrase, "twice the sum of a number and 5," opens a door to a fascinating exploration of mathematical concepts, problem-solving techniques, and surprisingly, real-world applications. Let's delve into this seemingly basic expression and uncover its hidden depths.
Understanding the Core Concept: Breaking Down the Phrase
At its heart, the phrase "twice the sum of a number and 5" describes a specific mathematical operation. Let's dissect it step-by-step:
- A number: This represents an unknown quantity, often denoted by a variable like x, y, or n.
- The sum of a number and 5: This means we add 5 to our unknown number (x + 5).
- Twice the sum: This instructs us to multiply the result of the previous step by 2 (2 * (x + 5)).
Therefore, the complete mathematical expression is 2(x + 5). This seemingly straightforward equation lays the groundwork for a variety of mathematical explorations and problem-solving scenarios.
Algebraic Manipulation and Simplification
The expression 2(x + 5) can be further simplified using the distributive property of multiplication over addition. This property states that for any numbers a, b, and c, a(b + c) = ab + ac. Applying this to our expression, we get:
2(x + 5) = 2x + 10
This simplified form, 2x + 10, is algebraically equivalent to the original expression and often proves more useful in solving equations or performing other mathematical operations. Understanding this equivalence is crucial for advanced mathematical concepts.
Solving Equations Involving "Twice the Sum of a Number and 5"
The expression "twice the sum of a number and 5" frequently appears within larger equations that need solving. Let's explore a few examples:
Example 1: A Simple Equation
Let's say we have the equation: 2(x + 5) = 14
To solve for x, we follow these steps:
- Distribute: 2x + 10 = 14
- Subtract 10 from both sides: 2x = 4
- Divide both sides by 2: x = 2
Therefore, the number is 2. We can verify this by substituting x = 2 back into the original equation: 2(2 + 5) = 2(7) = 14. The equation holds true.
Example 2: A More Complex Equation
Consider a more complex equation: 3(2(x + 5) - 7) = 21
Solving this involves multiple steps:
- Distribute the inner parentheses: 3(2x + 10 - 7) = 21
- Simplify the inner parentheses: 3(2x + 3) = 21
- Distribute the 3: 6x + 9 = 21
- Subtract 9 from both sides: 6x = 12
- Divide both sides by 6: x = 2
Again, we find that x = 2. This demonstrates how the expression "twice the sum of a number and 5" can be embedded within more complex mathematical structures.
Real-World Applications: Beyond the Textbook
While the expression may seem purely abstract, it has practical applications in various real-world scenarios:
1. Geometry and Area Calculations:
Imagine a rectangle with a length that is "twice the sum of its width and 5". If the width is represented by w, then the length would be 2(w + 5). Knowing the area of a rectangle (length * width), we can create and solve equations relating to area and dimensions.
2. Finance and Investment:
Consider a scenario where an investment grows by an amount that's "twice the sum of the initial investment and 5". Let the initial investment be i. The growth would then be 2(i + 5). This type of calculation is fundamental in understanding compound interest and investment growth.
3. Physics and Motion:
In physics, expressions similar to this can represent the displacement of an object under certain conditions, where the initial velocity or acceleration could be related to "twice the sum of a constant and a variable".
4. Everyday Scenarios:
Consider a situation where you're buying items. Let's say you buy x number of items costing $5 each, and then you buy two more additional items at a cost of $5. The total cost would be 2(x + 5).
Expanding the Concept: Introducing Inequalities
Instead of equations, we can also explore inequalities involving "twice the sum of a number and 5". For instance:
2(x + 5) > 10
Solving this inequality follows a similar process to solving equations, but with important distinctions:
- Distribute: 2x + 10 > 10
- Subtract 10 from both sides: 2x > 0
- Divide both sides by 2: x > 0
This means that x must be any number greater than 0 to satisfy the inequality. Understanding inequalities broadens the scope of problem-solving abilities.
Advanced Applications: Functions and Graphs
The expression 2(x + 5) can be represented as a function, f(x) = 2(x + 5) or f(x) = 2x + 10. This allows us to analyze its properties, such as its slope (2), y-intercept (10), and domain and range. Graphing this linear function provides a visual representation of the relationship between x and the expression's value. This visualization aids in understanding the behavior of the function and solving related problems.
Conclusion: A Foundation for Further Exploration
The phrase "twice the sum of a number and 5" may initially appear trivial, but its mathematical implications are surprisingly rich and diverse. From simple equation solving to complex inequalities and functional analysis, this expression serves as a fundamental building block for various mathematical concepts. Its applicability in real-world situations highlights the power of even seemingly basic mathematical principles. By understanding its underlying structure and manipulations, we build a strong foundation for tackling more challenging mathematical problems and gaining a deeper appreciation for the interconnectedness of mathematics and the real world. Further exploration into linear algebra, calculus, and other advanced mathematical fields will reveal even more sophisticated applications of this fundamental concept. Mastering this simple expression is key to unlocking a wider understanding of advanced mathematical concepts.
Latest Posts
Latest Posts
-
2 To The 3 To The 4
May 11, 2025
-
What Do The Four Terrestrial Planets Have In Common
May 11, 2025
-
50 Lb Of Sand In Cubic Feet
May 11, 2025
-
How Many Miles Does A Smart Car Last
May 11, 2025
-
Square Root Of 7 Rational Or Irrational
May 11, 2025
Related Post
Thank you for visiting our website which covers about Twice The Sum Of A Number And 5. . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.