What Do All Rectangles Have In Common
Arias News
Apr 06, 2025 · 5 min read
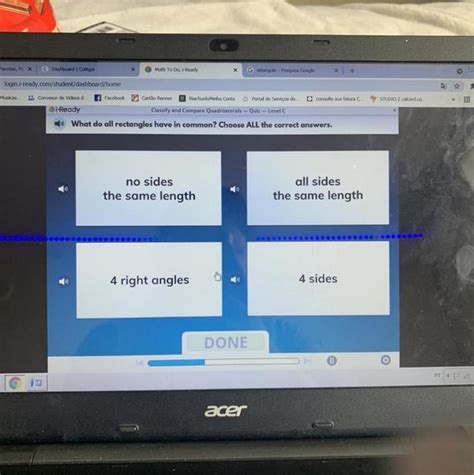
Table of Contents
What Do All Rectangles Have in Common? A Deep Dive into Quadrilateral Properties
Rectangles. We see them everywhere – in buildings, screens, paintings, and even in the arrangement of objects. But what exactly defines a rectangle? Beyond their familiar shape, what fundamental geometric properties unite all rectangles, regardless of their size or orientation? This article explores the defining characteristics of rectangles, delving into their properties and exploring their relationship to other quadrilaterals. We'll uncover the common threads that weave together this ubiquitous geometric figure.
Defining a Rectangle: The Foundation of Understanding
Before we delve into their shared characteristics, let's establish a precise definition. A rectangle is a quadrilateral (a four-sided polygon) with four right angles. This simple yet powerful definition is the bedrock upon which all other properties are built. This means every corner, or vertex, of a rectangle forms a 90-degree angle. This seemingly straightforward definition holds the key to understanding the numerous other properties that all rectangles inherently possess.
Key Properties: Shared by All Rectangles
The definition of a rectangle immediately implies several critical geometric properties. These properties are not merely consequences; they are inherent and inseparable aspects of what makes a shape a rectangle. Let's examine these properties:
-
Four Right Angles: This is the defining property. Every rectangle, without exception, possesses four angles, each measuring exactly 90 degrees. This is the cornerstone characteristic that distinguishes rectangles from other quadrilaterals.
-
Opposite Sides are Equal and Parallel: Because of the four right angles, the opposite sides of a rectangle are always congruent (equal in length) and parallel. This parallelism is crucial; it means the opposite sides will never intersect, no matter how far they are extended. This property ensures the stability and predictable nature of rectangles in various applications.
-
Diagonals Bisect Each Other: The diagonals of a rectangle (lines connecting opposite vertices) are not only equal in length but also bisect (divide into two equal parts) each other. The point where the diagonals intersect is the center of the rectangle, often used as a reference point in various geometric calculations and constructions.
-
Sum of Interior Angles: Like all quadrilaterals, the sum of the interior angles of a rectangle is always 360 degrees. Since each angle is already known to be 90 degrees, this property serves as a confirmation of the consistency of the shape's interior angles.
-
Area Calculation: The area of a rectangle is simply the product of its length and width. This straightforward formula (Area = length × width) makes it incredibly easy to calculate the area of any rectangle, given the lengths of its sides. This ease of calculation is one of the reasons why rectangular shapes are so frequently used in design and construction.
-
Perimeter Calculation: The perimeter of a rectangle (the total distance around its edges) is twice the sum of its length and width. This formula (Perimeter = 2 × (length + width)) allows for quick and accurate calculation of the total length of the rectangle's sides. Understanding the perimeter is essential in various applications, from framing a picture to designing a building layout.
Rectangles and Other Quadrilaterals: A Family Resemblance
Understanding the properties of rectangles allows us to explore their relationship with other quadrilaterals. Rectangles belong to a broader family of shapes, each with its own set of unique characteristics.
Rectangles as Special Cases:
-
Squares: A square is a special type of rectangle where all four sides are equal in length. This adds an extra layer of symmetry to the rectangle's properties, making it a highly regular polygon.
-
Parallelograms: A rectangle is a special case of a parallelogram. Parallelograms are quadrilaterals with opposite sides that are parallel and equal in length. However, parallelograms do not necessarily have right angles; rectangles are a subset of parallelograms with the added constraint of 90-degree angles.
-
Trapezoids (Trapeziums): While rectangles are not trapezoids, the relationship highlights the hierarchy of quadrilaterals. Trapezoids have at least one pair of parallel sides, but rectangles possess two pairs of parallel sides (making them a more specialized type of quadrilateral).
Real-World Applications: The Ubiquity of Rectangles
The prevalence of rectangles in our world speaks to their inherent practicality and efficiency. Their predictable properties make them ideal for countless applications:
-
Architecture and Construction: Buildings, rooms, windows, and doors are often rectangular in shape because of the ease of construction and the stability that rectangular frames provide.
-
Computer Screens and Displays: The rectangular shape of screens optimizes the display of images and text, making them suitable for various applications.
-
Packaging and Shipping: Rectangular boxes are widely used for packaging because they are space-efficient and easily stackable.
-
Furniture Design: Tables, chairs, beds, and cabinets often utilize rectangular shapes for stability, functionality, and ease of manufacturing.
-
Art and Design: Rectangles are frequently used in painting, graphic design, and photography to create balance, structure, and visual appeal.
Beyond the Basics: Advanced Properties and Concepts
While we've covered the fundamental properties, let's explore some more advanced concepts related to rectangles:
Area and Perimeter Optimization:
Given a fixed perimeter, a square (a special case of a rectangle) has the largest possible area. This principle has significant implications in design and engineering, where maximizing area within a given perimeter is often a crucial constraint.
Geometric Transformations:
Rectangles are easily transformed through rotations, reflections, and translations, which are important concepts in geometry and computer graphics. Understanding these transformations allows us to manipulate and analyze rectangles in different spatial contexts.
Three-Dimensional Extensions:
Extending the concept to three dimensions, we have rectangular prisms (also known as cuboids), which share many analogous properties with rectangles. Their volume, surface area, and diagonal calculations are extensions of the two-dimensional rectangular properties.
Conclusion: The Enduring Significance of Rectangles
From the simplest geometric definition to their complex applications in various fields, rectangles demonstrate a fascinating blend of simplicity and utility. Their inherent properties—four right angles, opposite sides equal and parallel, and bisecting diagonals—form the foundation of their widespread use. Understanding these properties not only provides a deeper appreciation for geometry but also illuminates the underlying principles behind the prevalence of rectangular shapes in the world around us. The seemingly mundane rectangle, therefore, reveals itself to be a remarkably significant and versatile geometric figure.
Latest Posts
Latest Posts
-
How Far Is Japan From California By Plane
Apr 07, 2025
-
What Happened When The Boarding House Blew Up Answers
Apr 07, 2025
-
How Many Minutes Are There In A Week
Apr 07, 2025
-
Can U Have Sex With A Dog
Apr 07, 2025
-
How Many Linear Feet In 1300 Square Feet
Apr 07, 2025
Related Post
Thank you for visiting our website which covers about What Do All Rectangles Have In Common . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.