What Does An Open Circle Mean In Math
Arias News
Mar 28, 2025 · 5 min read
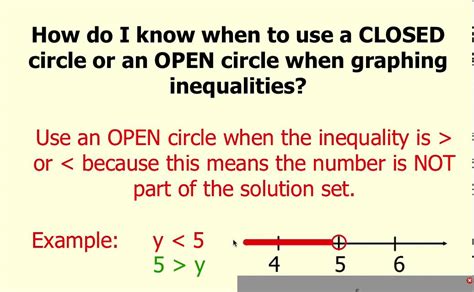
Table of Contents
What Does an Open Circle Mean in Math? A Comprehensive Guide
The humble open circle, seemingly insignificant in its simplicity, holds a powerful meaning within the world of mathematics. Understanding its implications is crucial for grasping fundamental concepts in algebra, calculus, and various other mathematical disciplines. This comprehensive guide will delve into the nuances of open circles, explaining their significance in different contexts and providing clear examples to solidify your understanding.
Open Circles in Number Lines and Inequalities
One of the most common uses of the open circle is in representing inequalities on a number line. Unlike a closed circle (or filled-in circle), which indicates inclusion, an open circle signifies exclusion. Let's explore this in detail:
Representing Inequalities
-
Less than (<) and Greater than (>): When dealing with inequalities involving "less than" (<) or "greater than" (>), an open circle is used on the number line to denote that the endpoint is not included in the solution set.
For example, if we have the inequality x > 3, we would place an open circle at the number 3 on the number line. This visually represents that x cannot equal 3, but it can be any value greater than 3. The line would extend to the right, indicating all values greater than 3.
-
Less than or equal to (≤) and Greater than or equal to (≥): Conversely, inequalities involving "less than or equal to" (≤) or "greater than or equal to" (≥) use a closed circle, indicating that the endpoint is included in the solution set.
For example, in the inequality x ≤ 5, a closed circle would be placed at 5 on the number line, showing that x can be 5 or any value less than 5.
Combining Inequalities: Compound Inequalities
Open circles play a crucial role when illustrating compound inequalities. Consider the compound inequality 2 < x < 7. This means x is greater than 2 and less than 7. On a number line, this would be represented by two open circles at 2 and 7, with a line segment connecting them. Both 2 and 7 are excluded from the solution set.
Real-World Applications
The concept of open circles in inequalities extends to numerous real-world applications:
- Temperature Ranges: If a recipe requires the oven temperature to be greater than 350°F, an open circle would represent 350°F on a visual representation of the acceptable temperature range.
- Speed Limits: A speed limit sign stating "Speed Limit: 65 mph" implies a less than or equal to situation (speed ≤ 65 mph). However, if a warning sign indicates a speed must exceed a certain limit for safety reasons (e.g., speed > 15 mph on a steep incline), an open circle would be relevant in its visual representation.
- Weight Restrictions: If a bridge has a weight limit of less than 10 tons, an open circle at 10 tons would visually represent the restriction on the number line.
Open Circles in Function Graphs
Open circles also appear in the graphs of functions to indicate points of discontinuity or holes. This signifies that the function is undefined at that specific point.
Points of Discontinuity
A function is discontinuous at a point where it is not continuous. There are several types of discontinuities, and an open circle often visually signifies a removable discontinuity (also known as a hole).
Let's consider a simple rational function: f(x) = (x² - 9) / (x - 3). If we try to evaluate f(3), we get 0/0, an indeterminate form. However, by factoring the numerator, we can simplify the function to f(x) = x + 3 for all x ≠ 3. The graph of this function would be a straight line with a slope of 1 and y-intercept of 3, but there would be an open circle at the point (3, 6), indicating that the function is undefined at x = 3.
Asymptotes
While not directly represented by an open circle, asymptotes (vertical, horizontal, or slant) are closely related to discontinuities. An asymptote is a line that a function approaches but never touches. The behavior of a function near an asymptote can be visualized using open circles to suggest the function's trend without actually reaching the asymptote.
Piecewise Functions
Piecewise functions, which are defined by different expressions over different intervals, often utilize open circles to clearly delineate the boundaries between the different pieces of the function. The open circle ensures that there is no ambiguity about which piece of the function applies at a given boundary point.
Open Circles in Set Theory
While less frequently used than in other mathematical contexts, open circles can subtly represent elements excluded from a set. This is especially relevant when visualizing set operations on a Venn diagram. While typically regions are shaded to represent sets, an open circle within a shaded region could theoretically signify a specific element excluded from the set despite the region's overall inclusion. This application is less common, but understanding its possibility is important for comprehensive understanding.
Open Circles vs. Closed Circles: A Direct Comparison
To emphasize the core difference, let's summarize the contrasting roles of open and closed circles:
| Feature | Open Circle | Closed Circle |
|---|---|---|
| Number Lines | Excludes the endpoint from the solution set | Includes the endpoint in the solution set |
| Inequalities | Used with < and > | Used with ≤ and ≥ |
| Function Graphs | Represents a point of discontinuity (hole) | Represents a point included in the graph |
| Set Theory | (Less common) Could denote exclusion | Denotes inclusion |
Advanced Applications and Nuances
As mathematical concepts become more complex, the interpretation of open circles can become nuanced. In advanced calculus, for example, understanding limits and continuity relies heavily on the subtle distinction between approaching a value (represented visually by an open circle's approach) and actually attaining it.
Conclusion
The humble open circle, despite its small size, communicates crucial information in mathematics. Mastering its meaning allows for a deeper understanding of inequalities, function graphs, and even set theory. By understanding its implications, students can move beyond mere calculation to a richer grasp of mathematical concepts and their real-world applications. Remember that open circles always signify exclusion, whether it is a point on a number line or a point of discontinuity on a function graph. This simple symbol serves as a powerful tool in visualizing and interpreting mathematical relationships. Through continued practice and exploration, the seemingly simple open circle will become a powerful tool in your mathematical toolbox.
Latest Posts
Latest Posts
-
How To Play The Recorder Hot Cross Buns
Mar 31, 2025
-
Protein In 8 Oz Chicken Breast Cooked
Mar 31, 2025
-
Why Is It Called A Handle Of Alcohol
Mar 31, 2025
-
How Long Does Egg Nog Last After Opening
Mar 31, 2025
-
How High Is A Story In A Building
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about What Does An Open Circle Mean In Math . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
