What Is 1 1/4 + 1 1/4
Arias News
Apr 11, 2025 · 6 min read
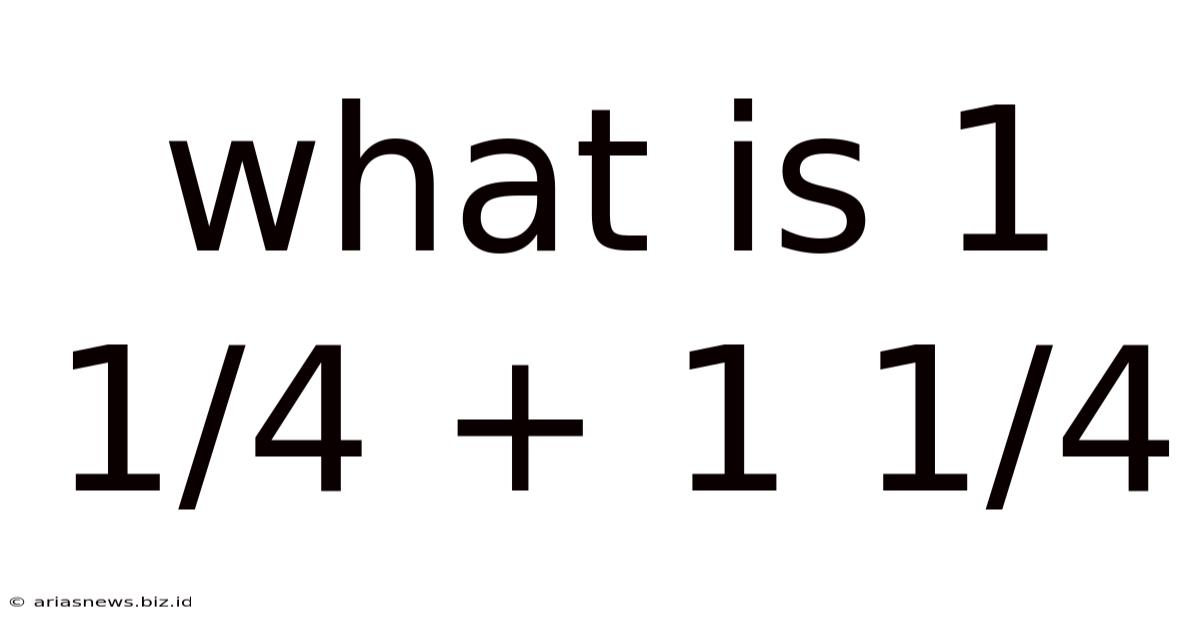
Table of Contents
- What Is 1 1/4 + 1 1/4
- Table of Contents
- What is 1 1/4 + 1 1/4? A Deep Dive into Fraction Addition and its Applications
- Understanding Fractions: A Quick Refresher
- Adding Fractions: A Step-by-Step Guide
- Alternative Approaches: Visualizing Fractions
- The Importance of Fractional Arithmetic in Real-World Applications
- Expanding on Fraction Addition: Different Scenarios
- Mastering Fractions: Tools and Resources
- Conclusion: The Significance of Foundational Math Skills
- Latest Posts
- Related Post
What is 1 1/4 + 1 1/4? A Deep Dive into Fraction Addition and its Applications
This seemingly simple question, "What is 1 1/4 + 1 1/4?", opens a door to a world of mathematical concepts crucial for various aspects of life. While the answer itself is straightforward, understanding the underlying principles of fraction addition provides a solid foundation for more complex mathematical operations and real-world problem-solving. This article will explore this addition problem in detail, explaining the process step-by-step, exploring different approaches, and highlighting the importance of fractional arithmetic in various fields.
Understanding Fractions: A Quick Refresher
Before diving into the addition problem, let's briefly review the fundamentals of fractions. A fraction represents a part of a whole. It consists of two numbers: the numerator (the top number) and the denominator (the bottom number). The denominator indicates how many equal parts the whole is divided into, while the numerator indicates how many of those parts are being considered.
For example, in the fraction 1/4, the denominator (4) signifies that the whole is divided into four equal parts, and the numerator (1) represents one of those four parts. Similarly, 1 1/4 represents one whole unit plus one quarter of a unit.
Adding Fractions: A Step-by-Step Guide
Adding fractions with the same denominator is relatively simple. You simply add the numerators and keep the denominator the same. Let's apply this to our problem: 1 1/4 + 1 1/4.
Step 1: Convert Mixed Numbers to Improper Fractions (Optional but Recommended):
A mixed number (like 1 1/4) consists of a whole number and a fraction. For easier addition, it's often helpful to convert mixed numbers into improper fractions. An improper fraction is one where the numerator is larger than or equal to the denominator.
To convert 1 1/4 to an improper fraction:
- Multiply the whole number (1) by the denominator (4): 1 * 4 = 4
- Add the numerator (1) to the result: 4 + 1 = 5
- Keep the same denominator (4): The improper fraction is 5/4.
Therefore, our problem becomes: 5/4 + 5/4
Step 2: Add the Numerators:
Since the denominators are the same, we simply add the numerators: 5 + 5 = 10
Step 3: Keep the Denominator:
The denominator remains the same: 4.
Step 4: Simplify the Result (If Necessary):
Our result is 10/4. This is an improper fraction. To simplify, we divide the numerator (10) by the denominator (4): 10 ÷ 4 = 2 with a remainder of 2. This can be expressed as a mixed number: 2 2/4.
Step 5: Further Simplification:
The fraction 2/4 can be simplified by dividing both the numerator and the denominator by their greatest common divisor (GCD), which is 2. This gives us 1/2.
Therefore, the final answer is 2 1/2.
Alternative Approaches: Visualizing Fractions
Understanding fractions can be enhanced by visualizing them. Imagine two pizzas, each cut into four equal slices. If you have one whole pizza and one-quarter of another (1 1/4), and then you add another one whole pizza and one-quarter (1 1/4), you'll have two whole pizzas and two quarters, which is equivalent to two and a half pizzas (2 1/2). This visual representation reinforces the mathematical calculation.
The Importance of Fractional Arithmetic in Real-World Applications
Fractional arithmetic isn't just a classroom exercise; it's a fundamental skill used across various professions and everyday life:
-
Cooking and Baking: Recipes often require fractional measurements of ingredients (e.g., 1 1/2 cups of flour, 1/4 teaspoon of salt). Accurate fractional calculations ensure the desired outcome.
-
Construction and Engineering: Precision is critical in construction and engineering. Fractions are used in measurements, calculations of materials needed, and the creation of blueprints.
-
Finance: Interest rates, loan calculations, and stock prices often involve fractions and decimals (which are closely related to fractions).
-
Data Analysis: Many data analysis techniques rely on understanding proportions and percentages, which are inherently connected to fractions.
-
Sewing and Tailoring: Accurate measurements and calculations using fractions are essential for creating well-fitting clothes.
-
Time Management: Understanding fractions of an hour (e.g., 1/4 hour = 15 minutes) helps in scheduling and time planning.
-
Everyday Shopping: Sales and discounts are often expressed as fractions (e.g., 1/3 off). Understanding these fractions helps consumers make informed purchasing decisions.
Expanding on Fraction Addition: Different Scenarios
While the initial problem was straightforward, let's explore scenarios involving fraction addition with varying complexities:
1. Adding Fractions with Different Denominators:
Adding fractions with different denominators requires finding a common denominator – a number that is a multiple of both denominators. For example, adding 1/3 + 1/4 involves finding the least common multiple (LCM) of 3 and 4, which is 12. Then, convert each fraction to an equivalent fraction with a denominator of 12 before adding the numerators.
2. Adding More Than Two Fractions:
Adding multiple fractions follows the same principle. First, find a common denominator for all fractions, then add the numerators. Simplify the result if necessary.
3. Adding Mixed Numbers with Different Denominators:
This combines the steps of converting mixed numbers to improper fractions and finding a common denominator. It's crucial to handle each step methodically.
4. Adding Fractions Involving Decimals:
It's possible to encounter problems that mix fractions and decimals. The best approach is usually to convert both to either fractions or decimals before performing the addition.
Mastering Fractions: Tools and Resources
Several resources can help improve your understanding and skills in fraction arithmetic:
-
Online Calculators: Many free online calculators can perform fraction addition and other fraction operations. However, it's crucial to understand the underlying principles rather than solely relying on calculators.
-
Educational Websites and Apps: Numerous websites and mobile apps offer interactive lessons and practice problems on fractions. These tools can be particularly helpful for visual learners.
-
Workbooks and Textbooks: Traditional workbooks and textbooks offer structured learning and practice exercises on fractions.
Conclusion: The Significance of Foundational Math Skills
The simple addition problem, 1 1/4 + 1 1/4, serves as a gateway to understanding the broader significance of fractional arithmetic. Mastery of fractions is not just about getting the right answer; it's about developing a deeper understanding of mathematical concepts that are essential for navigating various aspects of life, from everyday tasks to complex professional applications. By understanding the principles and practicing regularly, you can build a solid foundation in mathematics and confidently tackle more advanced problems. This foundational knowledge will serve you well in countless situations and empower you to solve problems with accuracy and efficiency.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is 1 1/4 + 1 1/4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.