What Is 1/2 Divided By 3 In Fraction Form
Arias News
May 12, 2025 · 5 min read
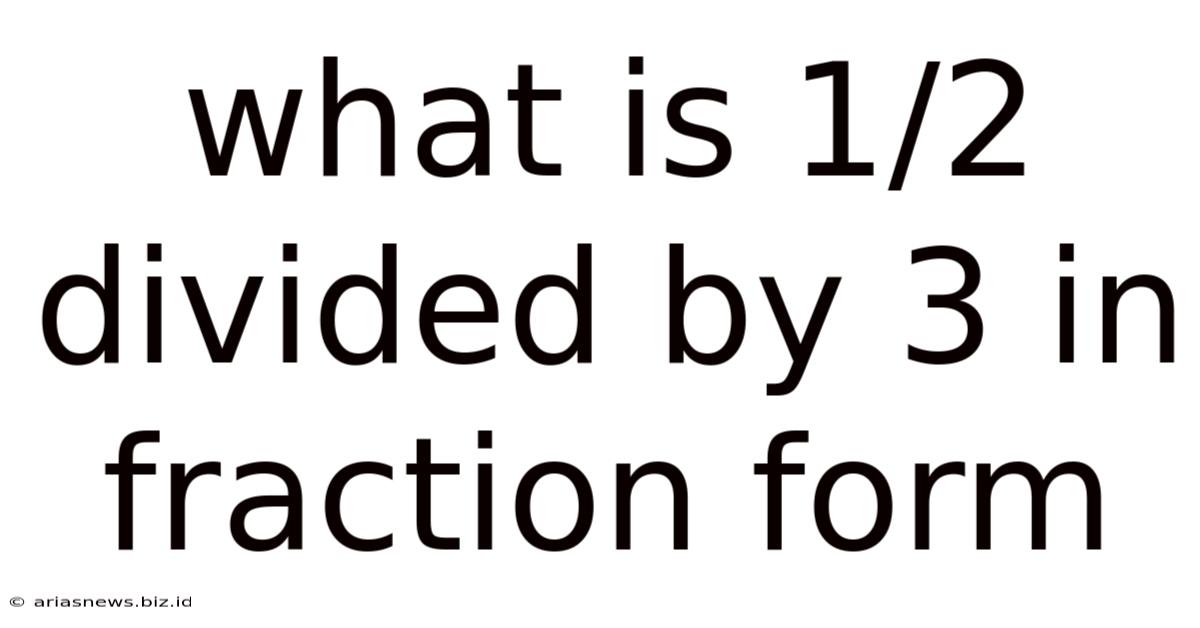
Table of Contents
What is 1/2 Divided by 3 in Fraction Form? A Comprehensive Guide
Understanding fraction division can be a stumbling block for many, but it's a fundamental skill in mathematics with wide-ranging applications. This comprehensive guide will walk you through the process of dividing fractions, specifically tackling the problem: What is 1/2 divided by 3 in fraction form? We'll explore the underlying concepts, provide step-by-step solutions, and delve into practical examples to solidify your understanding. By the end, you'll be confident in tackling similar fraction division problems.
Understanding Fraction Division
Before we jump into solving 1/2 ÷ 3, let's review the basics of fraction division. Dividing by a fraction is essentially the same as multiplying by its reciprocal. The reciprocal of a fraction is simply the fraction flipped upside down. For example, the reciprocal of 2/3 is 3/2.
The process can be summarized as follows:
-
Identify the dividend and the divisor: In the problem a/b ÷ c/d, a/b is the dividend and c/d is the divisor.
-
Find the reciprocal of the divisor: Flip the divisor fraction upside down.
-
Multiply the dividend by the reciprocal of the divisor: (a/b) × (d/c)
-
Simplify the resulting fraction: Reduce the fraction to its lowest terms if possible.
Solving 1/2 Divided by 3
Now, let's apply these steps to our problem: 1/2 ÷ 3.
First, we need to express the whole number 3 as a fraction. Any whole number can be written as a fraction with a denominator of 1. Therefore, 3 can be written as 3/1.
Our problem now becomes: 1/2 ÷ 3/1
Following the steps outlined above:
- Dividend: 1/2
- Divisor: 3/1
- Reciprocal of the divisor: 1/3
- Multiplication: (1/2) × (1/3)
To multiply fractions, we multiply the numerators together and the denominators together:
(1 × 1) / (2 × 3) = 1/6
Therefore, 1/2 divided by 3 is 1/6.
Visualizing the Solution
It can be helpful to visualize fraction division. Imagine you have half a pizza (1/2). You want to divide this half pizza into three equal portions. Each portion will be significantly smaller than the original half pizza. This smaller portion represents 1/6 of the whole pizza.
Alternative Approach: Using the KCF Method (Keep, Change, Flip)
Another way to remember how to divide fractions is the KCF method: Keep, Change, Flip.
- Keep: Keep the first fraction (the dividend) as it is.
- Change: Change the division sign (÷) to a multiplication sign (×).
- Flip: Flip the second fraction (the divisor) to its reciprocal.
Applying this method to 1/2 ÷ 3:
- Keep: 1/2
- Change: ÷ becomes ×
- Flip: 3/1 becomes 1/3
The problem now becomes: (1/2) × (1/3) = 1/6
Practical Applications of Fraction Division
Fraction division isn't just a theoretical concept; it's used extensively in various real-world scenarios:
-
Cooking and Baking: Recipes often require dividing ingredients. For example, if a recipe calls for 1/2 cup of flour and you want to make 1/3 of the recipe, you'd need to calculate 1/2 ÷ 3 = 1/6 cup of flour.
-
Sewing and Tailoring: Cutting fabric for garments involves precise measurements. Dividing lengths of fabric into smaller pieces often necessitates fraction division.
-
Construction and Engineering: Precise measurements and calculations are crucial in construction and engineering. Dividing lengths, volumes, or weights frequently involves fraction division.
-
Data Analysis: When dealing with proportions and percentages, fraction division is commonly used.
-
Financial Calculations: Many financial calculations, such as calculating interest rates or shares, involve fraction division.
Expanding on Fraction Division: More Complex Examples
Let's explore a few more complex examples to further solidify your understanding of fraction division:
Example 1: 2/3 ÷ 4/5
- Keep: 2/3
- Change: ÷ becomes ×
- Flip: 4/5 becomes 5/4
(2/3) × (5/4) = (2 × 5) / (3 × 4) = 10/12
Simplifying the fraction: 10/12 = 5/6
Therefore, 2/3 ÷ 4/5 = 5/6
Example 2: 3 1/2 ÷ 2
First, convert the mixed number 3 1/2 into an improper fraction: (3 × 2 + 1) / 2 = 7/2
Now, the problem is 7/2 ÷ 2/1
- Keep: 7/2
- Change: ÷ becomes ×
- Flip: 2/1 becomes 1/2
(7/2) × (1/2) = 7/4
Converting the improper fraction back to a mixed number: 7/4 = 1 3/4
Therefore, 3 1/2 ÷ 2 = 1 3/4
Example 3: 1/4 ÷ 2/5 ÷ 1/3
This involves multiple divisions. We work from left to right:
First, 1/4 ÷ 2/5:
(1/4) × (5/2) = 5/8
Next, 5/8 ÷ 1/3:
(5/8) × (3/1) = 15/8
Therefore, 1/4 ÷ 2/5 ÷ 1/3 = 15/8 (or 1 7/8)
Troubleshooting Common Mistakes
Here are some common mistakes to avoid when dividing fractions:
-
Forgetting to find the reciprocal: Remember to flip the second fraction (the divisor) before multiplying.
-
Incorrectly multiplying numerators and denominators: Always multiply the numerators together and the denominators together separately.
-
Not simplifying the result: Always reduce the resulting fraction to its simplest form.
By understanding the principles of fraction division and practicing with various examples, you can confidently solve any fraction division problem, even those beyond the simple 1/2 ÷ 3. Remember the KCF method, and visualize the problem to reinforce your understanding. With consistent practice, fraction division will become second nature.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is 1/2 Divided By 3 In Fraction Form . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.