What Is 10 To The Negative 2nd Power
Arias News
May 12, 2025 · 4 min read
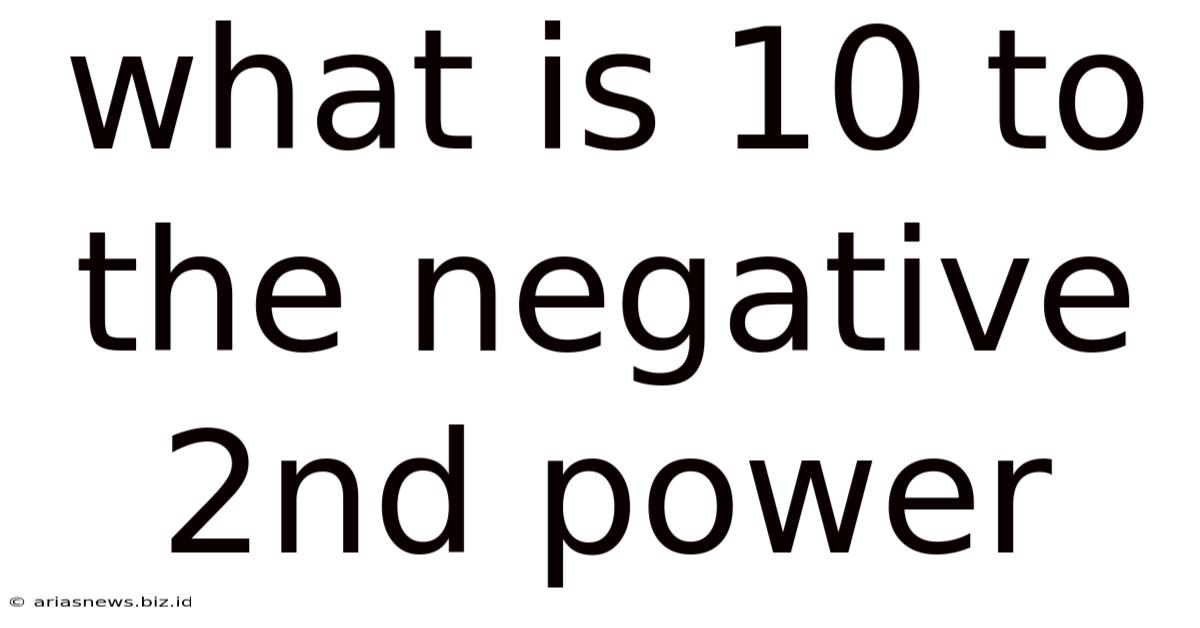
Table of Contents
What is 10 to the Negative 2nd Power? A Deep Dive into Exponents and Scientific Notation
Understanding exponents, especially negative exponents, is crucial for anyone working with numbers, from basic arithmetic to advanced scientific calculations. This comprehensive guide will explore the meaning of 10 to the negative 2nd power (10⁻²), delve into the underlying principles of exponents, and demonstrate its practical applications in various fields. We'll cover everything from the basic definition to its relevance in scientific notation and real-world scenarios.
Understanding Exponents: The Fundamentals
Before diving into negative exponents, let's solidify our understanding of exponents in general. An exponent, also known as a power or index, indicates how many times a base number is multiplied by itself. For example:
- 10² means 10 multiplied by itself twice: 10 * 10 = 100
- 5³ means 5 multiplied by itself three times: 5 * 5 * 5 = 125
The general form is bⁿ, where 'b' represents the base and 'n' represents the exponent.
Positive Exponents: A Quick Recap
Positive exponents represent repeated multiplication. The larger the positive exponent, the larger the resulting number. For instance:
- 10¹ = 10
- 10² = 100
- 10³ = 1000
- 10⁴ = 10000
This pattern shows a clear relationship: each increase in the exponent adds another zero to the end of the number (when the base is 10).
Negative Exponents: The Flip Side
Now, let's tackle negative exponents. A negative exponent doesn't signify a negative number; instead, it indicates the reciprocal of the base raised to the positive power. In simpler terms, it means "1 divided by" the base raised to the positive exponent.
Therefore, 10⁻² is equivalent to 1 / 10² = 1 / (10 * 10) = 1 / 100 = 0.01
Calculating 10 to the Negative 2nd Power
Let's break down the calculation step-by-step:
-
Identify the base and exponent: The base is 10, and the exponent is -2.
-
Apply the rule for negative exponents: The negative exponent signifies the reciprocal.
-
Calculate the positive exponent: 10² = 100
-
Take the reciprocal: 1 / 100 = 0.01
Therefore, 10⁻² = 0.01
Scientific Notation: The Power of 10⁻²
Scientific notation is a way of representing very large or very small numbers concisely using powers of 10. It's particularly useful in science and engineering where numbers often involve many digits. The general form is:
a x 10ⁿ
Where 'a' is a number between 1 and 10 (but not including 10), and 'n' is an integer (positive, negative, or zero) representing the power of 10.
10⁻² in Scientific Notation
While 0.01 isn't technically in scientific notation (as the 'a' value is not between 1 and 10), it's often a component within larger numbers expressed in scientific notation. For example:
- 2.5 x 10⁻² = 2.5 x 0.01 = 0.025
- 7.8 x 10⁻² = 7.8 x 0.01 = 0.078
Here, 10⁻² acts as a multiplier, shifting the decimal point two places to the left.
Real-world Applications of 10⁻²
10⁻² and the concept of negative exponents have numerous real-world applications:
-
Chemistry: Expressing concentrations of solutions. For example, a 0.01 M (molar) solution can be written as 1 x 10⁻² M.
-
Physics: Representing small measurements such as the wavelength of light or the charge of an electron.
-
Engineering: Dealing with tiny tolerances or dimensions in microelectronics.
-
Finance: Calculating small percentages or interest rates. For instance, 1% can be expressed as 0.01 or 1 x 10⁻².
-
Everyday life: Consider the size of a dust mite which is often measured in millimeters or even micrometers – values commonly expressed using negative exponents.
Beyond 10⁻²: Exploring Other Negative Exponents
The concept extends beyond 10⁻². Let's consider other examples:
-
10⁻¹: This equals 1 / 10¹ = 1 / 10 = 0.1
-
10⁻³: This equals 1 / 10³ = 1 / 1000 = 0.001
-
10⁻⁴: This equals 1 / 10⁴ = 1 / 10000 = 0.0001
Notice the pattern: each decrease in the negative exponent adds another zero to the left of the decimal point in the decimal representation.
Working with Negative Exponents: Key Rules and Properties
-
Product Rule: When multiplying numbers with the same base, add the exponents: 10³ * 10⁻² = 10⁽³⁻²⁾ = 10¹ = 10
-
Quotient Rule: When dividing numbers with the same base, subtract the exponents: 10⁵ / 10⁻² = 10⁽⁵⁻⁽⁻²⁾⁾ = 10⁷ = 10,000,000
-
Power Rule: When raising a power to another power, multiply the exponents: (10⁻²)³ = 10⁽⁻²*³⁾ = 10⁻⁶ = 0.000001
-
Zero Exponent: Any number (except zero) raised to the power of zero is 1: 10⁰ = 1
Mastering Negative Exponents: Practical Exercises
Practice is key to mastering negative exponents. Try solving these examples:
-
Calculate 5⁻².
-
Express 0.0000001 in scientific notation.
-
Simplify (2 x 10⁻³) * (4 x 10⁵).
-
Convert 10⁻⁵ into a decimal.
Conclusion: The Significance of 10⁻² and Negative Exponents
Understanding 10⁻² and negative exponents is fundamental for navigating various mathematical and scientific contexts. From its role in scientific notation to its applications in diverse fields, mastering this concept enhances our ability to handle numbers effectively and interpret complex data. By applying the rules and principles discussed here, you can confidently tackle any problems involving negative exponents and unlock a deeper comprehension of the numerical world. Remember to practice regularly to solidify your understanding and make this essential concept second nature.
Latest Posts
Latest Posts
-
How To Address A Letter To A Nursing Home Resident
May 12, 2025
-
Can Bearded Dragons Eat Brussel Sprout Leaves
May 12, 2025
-
How Many Right Angles Does Trapezoid Have
May 12, 2025
-
Kohler 52 50 02 S Cross Reference
May 12, 2025
-
How Much Is 1 Acre Of Land In Mexico
May 12, 2025
Related Post
Thank you for visiting our website which covers about What Is 10 To The Negative 2nd Power . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.