What Is 10 To The Negative 4 Power
Arias News
May 09, 2025 · 5 min read
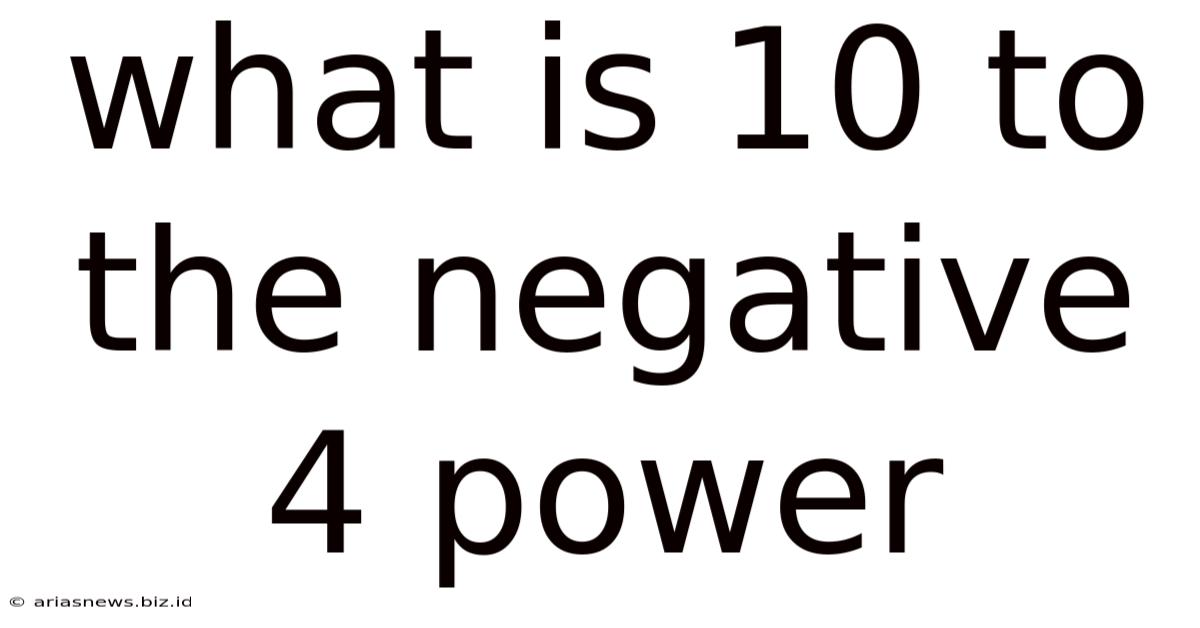
Table of Contents
What is 10 to the Negative 4 Power? A Comprehensive Guide
Understanding exponents, especially negative ones, can sometimes feel daunting. But mastering this concept is crucial for various fields, from science and engineering to finance and everyday calculations. This comprehensive guide will delve deep into the meaning of 10 to the negative 4 power (10<sup>-4</sup>), explaining its value, applications, and broader implications within the realm of scientific notation and exponential functions.
Deconstructing the Power of Ten
Before we tackle 10<sup>-4</sup> specifically, let's establish a solid foundation in understanding exponents and negative exponents.
Understanding Exponents
An exponent (or power) indicates how many times a number (the base) is multiplied by itself. For example:
- 10<sup>2</sup> (10 squared) means 10 × 10 = 100
- 10<sup>3</sup> (10 cubed) means 10 × 10 × 10 = 1000
- 10<sup>5</sup> means 10 × 10 × 10 × 10 × 10 = 100,000
Notice a pattern? The exponent tells us the number of zeros after the '1' when the base is 10.
Understanding Negative Exponents
Negative exponents represent the reciprocal of the positive exponent. In simpler terms, it flips the fraction.
- 10<sup>-1</sup> is the reciprocal of 10<sup>1</sup>, which is 1/10 = 0.1
- 10<sup>-2</sup> is the reciprocal of 10<sup>2</sup>, which is 1/100 = 0.01
- 10<sup>-3</sup> is the reciprocal of 10<sup>3</sup>, which is 1/1000 = 0.001
This reciprocal relationship is key to understanding negative exponents. The negative sign doesn't make the number negative; it indicates a fractional value.
Calculating 10 to the Negative 4 Power
Now, let's directly address the question: what is 10<sup>-4</sup>?
Following the pattern of negative exponents, 10<sup>-4</sup> is the reciprocal of 10<sup>4</sup>. 10<sup>4</sup> is 10,000 (ten thousand). Therefore:
10<sup>-4</sup> = 1/10,000 = 0.0001
This means 10 to the negative 4 power is equal to one ten-thousandth.
The Significance of Scientific Notation
Scientific notation is a way of expressing very large or very small numbers concisely. It utilizes powers of 10 to represent these numbers efficiently. 10<sup>-4</sup> is a prime example of its use in representing small quantities.
For instance, the diameter of a typical human hair might be expressed as 0.0001 meters. In scientific notation, this is written as 1 x 10<sup>-4</sup> meters. This notation avoids the cumbersome use of many zeros, making the number easier to read, write, and work with in calculations.
Real-World Applications of 10<sup>-4</sup>
The application of 10<sup>-4</sup> and similar small values in scientific notation is vast, spanning numerous fields:
1. Physics and Engineering:
- Measurement of small distances: As mentioned above, measuring the diameter of a hair or the wavelength of light often involves numbers in the 10<sup>-4</sup> range.
- Electrical Engineering: Understanding currents, voltages, and resistances often requires working with extremely small values.
- Mechanical Engineering: Tolerance levels in manufacturing processes are frequently expressed using powers of 10, including 10<sup>-4</sup>.
2. Chemistry:
- Molarity and concentration: Expressing the concentration of solutions often uses scientific notation, frequently involving exponents like -4.
- Chemical reactions: The amounts of reactants and products in chemical reactions can sometimes be expressed using extremely small numbers represented by powers of 10.
3. Biology:
- Microscopic measurements: Measuring the sizes of cells, bacteria, and viruses frequently requires values in the range of 10<sup>-4</sup> to 10<sup>-6</sup>.
- Genetic analysis: The probability of specific genetic events can involve extremely small numbers, commonly expressed using scientific notation.
4. Finance and Economics:
- Interest rates and percentage changes: While not always directly using 10<sup>-4</sup>, the concepts of percentages and decimals used in finance are closely related to exponential notation.
- Statistical analysis: Many statistical models and calculations use exponential notations to represent probabilities and other values.
Beyond 10<sup>-4</sup>: Exploring Other Negative Exponents
Understanding 10<sup>-4</sup> provides a solid foundation for grasping other negative exponents. Let's briefly explore some related values:
- 10<sup>-1</sup> (0.1): One tenth; commonly used in expressing percentages or decimal fractions.
- 10<sup>-2</sup> (0.01): One hundredth; frequently used in expressing percentages and representing small fractions.
- 10<sup>-3</sup> (0.001): One thousandth; relevant in various scientific measurements and calculations.
- 10<sup>-5</sup> (0.00001): One hundred-thousandth; used for extremely small measurements and concentrations.
- 10<sup>-6</sup> (0.000001): One millionth; common in microbiology and nanotechnology.
Mastering Negative Exponents: Tips and Tricks
Here are some helpful strategies to improve your understanding and calculations involving negative exponents:
- Practice regularly: The more you work with exponents, the more comfortable you'll become.
- Utilize online resources: Numerous websites and calculators can assist with exponent calculations.
- Break down complex problems: Tackle large problems by breaking them into smaller, manageable steps.
- Understand the reciprocal relationship: Remember that a negative exponent is simply the reciprocal of its positive counterpart.
- Visualize the decimal places: Associate negative exponents with the number of decimal places (to the right of the decimal point).
Conclusion: The Power of Small Numbers
10 to the negative 4 power, while seemingly insignificant as a numerical value, holds profound significance in many scientific, engineering, and everyday applications. Mastering this concept provides a critical stepping stone to understanding exponential notation, scientific notation, and the manipulation of very small (and very large) quantities. Its role in expressing and interpreting data across diverse fields underscores its importance in our understanding of the world around us. By understanding its implications, you not only enhance your mathematical capabilities but also gain a deeper appreciation for the power of small numbers in a vast universe.
Latest Posts
Latest Posts
-
How Did Stalin Use Propaganda To Control His People Apex
May 09, 2025
-
How Do You Find The Radius Of A Cylinder
May 09, 2025
-
How Long Is 15 Mm In Inches
May 09, 2025
-
How Old Was Queen Esther When She Died
May 09, 2025
-
How Far Is California From Phoenix Arizona
May 09, 2025
Related Post
Thank you for visiting our website which covers about What Is 10 To The Negative 4 Power . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.