What Is 10 To The Sixth Power
Arias News
May 09, 2025 · 5 min read
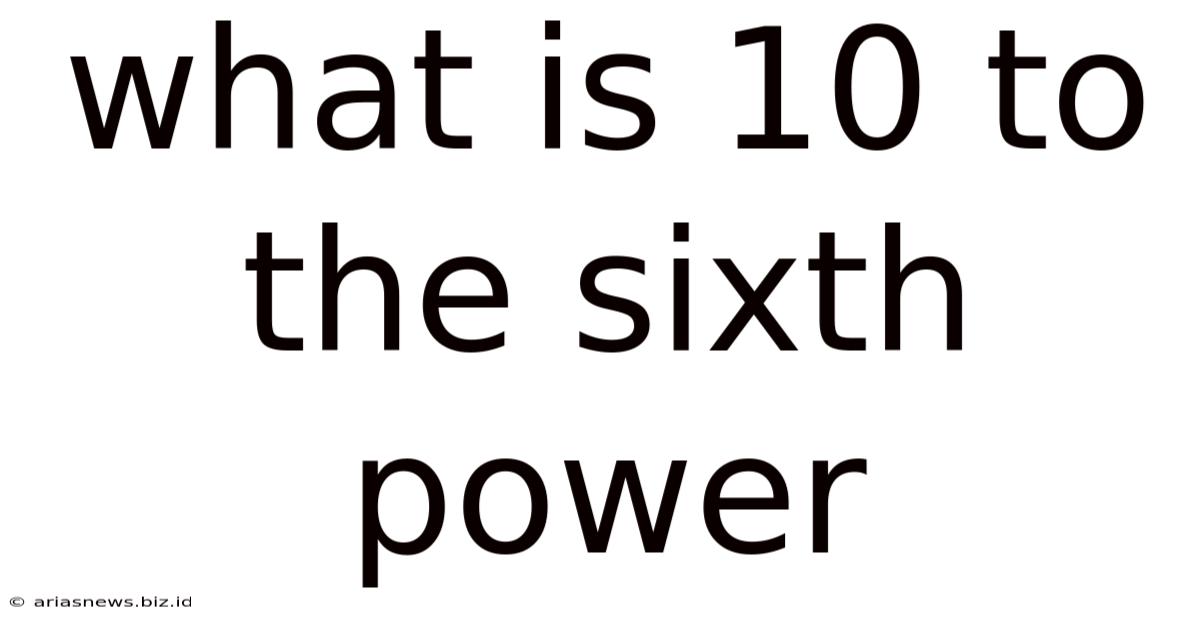
Table of Contents
What is 10 to the Sixth Power? A Deep Dive into Exponents and Scientific Notation
Understanding exponents, particularly those involving the number 10, is fundamental to grasping many scientific concepts and performing complex calculations. This comprehensive guide will explore the meaning of 10 to the sixth power (10⁶), its applications, and its broader significance in mathematics and science. We'll cover not just the answer, but the why behind it, equipping you with a solid understanding of exponential notation and its practical uses.
Deciphering the Language of Exponents
Before we tackle 10 to the sixth power, let's establish a solid foundation in exponential notation. An exponent, also known as a power or index, indicates how many times a number (the base) is multiplied by itself. For example:
- 2³ = 2 × 2 × 2 = 8 (2 raised to the power of 3, or 2 cubed)
- 5² = 5 × 5 = 25 (5 raised to the power of 2, or 5 squared)
The general form is bⁿ, where 'b' is the base and 'n' is the exponent. This expression means 'b' multiplied by itself 'n' times.
Calculating 10 to the Sixth Power (10⁶)
Now, let's focus on the specific question: What is 10 to the sixth power? This means multiplying 10 by itself six times:
10⁶ = 10 × 10 × 10 × 10 × 10 × 10 = 1,000,000
Therefore, 10 to the sixth power is equal to one million.
The Significance of Powers of 10
Powers of 10 (10¹, 10², 10³, etc.) are particularly significant in mathematics and science because they provide a simple and efficient way to represent very large and very small numbers. This is the basis of scientific notation, a crucial tool for expressing numbers concisely and managing their scale.
Understanding Scientific Notation
Scientific notation expresses a number as a product of a number between 1 and 10 (the coefficient) and a power of 10. For instance:
- 3,000,000 can be written as 3 × 10⁶
- 0.00005 can be written as 5 × 10⁻⁵
The exponent in scientific notation tells us how many places the decimal point needs to be moved to obtain the standard form of the number. A positive exponent indicates a large number (decimal point moves to the right), while a negative exponent indicates a small number (decimal point moves to the left).
Applications of 10 to the Sixth Power and Scientific Notation
The ability to represent and manipulate large numbers using exponents and scientific notation is invaluable in various fields:
1. Astronomy: Measuring Vast Distances
Astronomy deals with incredibly large distances. Light-years, the distance light travels in a year, are often expressed using scientific notation. Understanding powers of 10 is crucial for interpreting distances between stars, galaxies, and other celestial bodies. For instance, a distance expressed as 10⁶ kilometers is easily comprehensible as one million kilometers.
2. Computing: Data Storage and Processing
The capacity of computer storage devices (hard drives, SSDs) is often expressed in gigabytes (GB) or terabytes (TB). These units are powers of 10. A terabyte, for example, is 10¹² bytes (1 trillion bytes), demonstrating the practical use of large exponents in the realm of computer science.
3. Finance: Handling Large Sums of Money
In finance, dealing with large amounts of money is commonplace. National budgets, global markets, and international trade involve numbers in the millions, billions, and even trillions. Scientific notation simplifies the representation and calculation of these massive figures, making them easier to understand and analyze.
4. Chemistry: Avogadro's Number and Moles
Avogadro's number (approximately 6.022 × 10²³), a fundamental constant in chemistry, represents the number of particles (atoms, molecules) in one mole of a substance. Scientific notation makes this incredibly large number manageable and simplifies calculations in stoichiometry (chemical calculations based on the relative quantities of reactants and products).
5. Biology: Microbial Populations and Cell Sizes
Biology often involves dealing with extremely large numbers (like microbial populations) or incredibly small measurements (like cell sizes). Scientific notation facilitates expressing these values concisely and accurately, enabling comparison and analysis of biological data.
Beyond 10⁶: Exploring Other Exponents
While we've focused on 10⁶, understanding other exponents of 10 is equally important. Let's explore a few more:
- 10⁰ = 1: Any number raised to the power of zero is 1.
- 10¹ = 10: The first power of any number is the number itself.
- 10² = 100: 10 squared, or 10 to the power of 2, is 100.
- 10³ = 1000: 10 cubed, or 10 to the power of 3, is 1000.
- 10⁴ = 10,000: 10 to the power of 4 is 10,000 (ten thousand).
- 10⁵ = 100,000: 10 to the power of 5 is 100,000 (one hundred thousand).
- 10⁷ = 10,000,000: 10 to the power of 7 is 10,000,000 (ten million).
- 10⁸ = 100,000,000: 10 to the power of 8 is 100,000,000 (one hundred million).
- And so on...
Understanding the pattern and the progression in these powers of 10 is crucial for grasping the scale of numbers and effectively utilizing scientific notation.
Negative Exponents and Very Small Numbers
So far, we've dealt with positive exponents. However, exponents can also be negative. A negative exponent indicates the reciprocal of the positive exponent. For example:
- 10⁻¹ = 1/10 = 0.1
- 10⁻² = 1/10² = 1/100 = 0.01
- 10⁻³ = 1/10³ = 1/1000 = 0.001
Negative exponents are particularly useful for representing very small numbers, such as those encountered in atomic physics, nanotechnology, and microbiology.
Mastering Exponents: A Key Mathematical Skill
Proficiency in working with exponents, particularly powers of 10, is a cornerstone of mathematical literacy. It significantly simplifies complex calculations, allows for clear representation of vast scales, and is indispensable across various scientific disciplines. Understanding the concepts explained in this article will enhance your problem-solving skills and broaden your comprehension of the world around us, from the immensity of the cosmos to the intricacies of the microscopic world. Practice regularly and explore more advanced concepts to solidify your understanding and unlock the power of exponential notation.
Latest Posts
Latest Posts
-
How Many Minutes Are In 100 Seconds
May 09, 2025
-
You And Your Family Are In My Prayers
May 09, 2025
-
2 Cups Of Sour Cream In Oz
May 09, 2025
-
10mm Is Equal To How Many Inches
May 09, 2025
-
How Far Can A 2x6 Rafter Span
May 09, 2025
Related Post
Thank you for visiting our website which covers about What Is 10 To The Sixth Power . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.