What Is 12 To The 0 Power
Arias News
May 08, 2025 · 5 min read
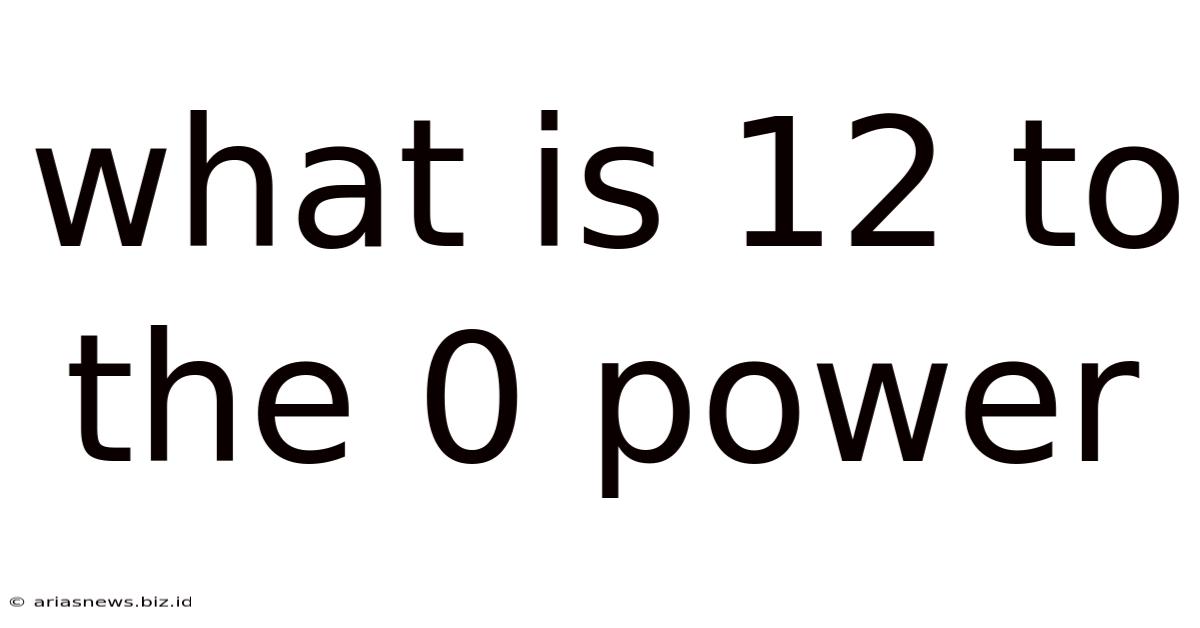
Table of Contents
What is 12 to the 0 Power? Understanding Exponents and the Zero Exponent Rule
The question, "What is 12 to the 0 power?" might seem deceptively simple, but it touches upon a fundamental concept in mathematics: exponents and the zero exponent rule. Understanding this rule requires delving into the logic behind exponents and their properties. This comprehensive guide will not only answer the question directly but also provide a thorough explanation of the underlying principles, addressing common misconceptions and solidifying your understanding of exponential notation.
Understanding Exponents
Before tackling the zero exponent, let's establish a solid foundation in exponents. An exponent, also known as a power or index, indicates how many times a number (the base) is multiplied by itself. For example:
- 3² = 3 × 3 = 9 (3 raised to the power of 2, or 3 squared)
- 5³ = 5 × 5 × 5 = 125 (5 raised to the power of 3, or 5 cubed)
- 2⁴ = 2 × 2 × 2 × 2 = 16 (2 raised to the power of 4)
In general, we represent this as: bⁿ = b × b × b × ... × b (n times), where 'b' is the base and 'n' is the exponent.
Exploring the Patterns of Exponents
Let's examine a pattern using the base number 2:
- 2⁴ = 16
- 2³ = 8
- 2² = 4
- 2¹ = 2
Notice that as the exponent decreases by 1, the result is divided by the base (2). This consistent pattern is crucial to understanding the zero exponent.
The Zero Exponent Rule: Why Anything to the Power of Zero is 1
Following the pattern established above, if we continue the sequence:
- 2¹ = 2
- 2⁰ = ?
To maintain the pattern of dividing by the base (2), we would have:
- 2¹ / 2 = 2⁰ = 1
Therefore, 2⁰ = 1. This isn't a coincidence; it's a direct consequence of the consistent pattern observed when decreasing exponents. This logic applies to any non-zero base. Any non-zero number raised to the power of zero equals 1.
Formal Proof of the Zero Exponent Rule
A more formal approach uses the properties of exponents, specifically the rule: bᵐ / bⁿ = b⁽ᵐ⁻ⁿ⁾.
Let's consider the expression b⁰ where 'b' is a non-zero number. We can rewrite b⁰ as b^(n-n) where 'n' is any integer. Using the exponent rule mentioned above:
b⁰ = b⁽ⁿ⁻ⁿ⁾ = bⁿ / bⁿ
Since any number divided by itself equals 1 (except for 0), we have:
b⁰ = 1
This provides a rigorous mathematical proof for the zero exponent rule.
Addressing the Case of 0⁰
The expression 0⁰ is a special case and is considered an indeterminate form. It doesn't have a single defined value because it leads to conflicting results depending on the approach taken. While it is often stated as undefined, its context within limits and calculus can lead to different results based on the limiting function. The discussion of 0⁰ is more complex and is typically covered in advanced mathematics.
The Importance of the Zero Exponent Rule
The zero exponent rule is crucial in various mathematical contexts, including:
- Algebraic manipulations: Simplifying expressions and solving equations often involve applying this rule.
- Polynomial functions: The constant term in a polynomial (the term without a variable) can be represented using the zero exponent rule (e.g., 5x² + 2x⁰ = 5x² + 2).
- Calculus: The rule plays a role in certain derivations and integral calculations.
- Scientific notation: Writing very large or very small numbers efficiently uses exponents, where the zero exponent can simplify calculations.
Solving the Problem: 12⁰
Now, we can confidently answer the initial question: What is 12 to the 0 power?
Based on the zero exponent rule, 12⁰ = 1.
Common Misconceptions and How to Avoid Them
Some common misunderstandings regarding the zero exponent include:
- Thinking 12⁰ equals 0: This is incorrect. Any non-zero number raised to the power of zero always equals 1.
- Assuming there's a special exception for 12: The zero exponent rule applies universally to all non-zero bases.
Expanding Your Understanding: Negative Exponents
While not directly related to the zero exponent, understanding negative exponents helps complete the picture of exponential notation. A negative exponent indicates the reciprocal of the positive exponent:
- b⁻ⁿ = 1/bⁿ
For example:
- 2⁻³ = 1/2³ = 1/8
Understanding negative exponents further reinforces the pattern and logic behind the zero exponent rule.
Practical Applications: Real-world Examples
The zero exponent rule might seem abstract, but it has practical applications in several fields:
- Computer Science: In algorithms and data structures, exponential growth or decay is often modeled, requiring understanding exponents, including the zero exponent.
- Finance: Compound interest calculations frequently use exponential functions. Understanding exponents helps in interpreting financial models.
- Physics: Many physical phenomena, such as radioactive decay, involve exponential relationships.
Conclusion: Mastering the Zero Exponent Rule
The concept of "What is 12 to the 0 power?" opens the door to a deeper understanding of exponents. By grasping the pattern of decreasing exponents, the logic behind the zero exponent rule becomes clear and intuitive. The rule, while seemingly simple, is a fundamental building block in various mathematical disciplines and real-world applications. Remember, for any non-zero base 'b', b⁰ = 1. Mastering this rule strengthens your foundation in mathematics and allows you to tackle more complex problems confidently. Through consistent practice and a solid understanding of the underlying principles, you can confidently navigate the world of exponents and their various applications.
Latest Posts
Latest Posts
-
Two Or More Objects Or Ideas Observed For Their Similarities
May 09, 2025
-
Are Nail Salons Open On New Years Day
May 09, 2025
-
Some People When They Are Caught In A Situation
May 09, 2025
-
What Does Away In The Launcher Mean In Fortnite
May 09, 2025
-
How Do You Say Do You Work Tomorrow In Spanish
May 09, 2025
Related Post
Thank you for visiting our website which covers about What Is 12 To The 0 Power . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.