What Is 12 To The Power Of 3
Arias News
May 11, 2025 · 5 min read
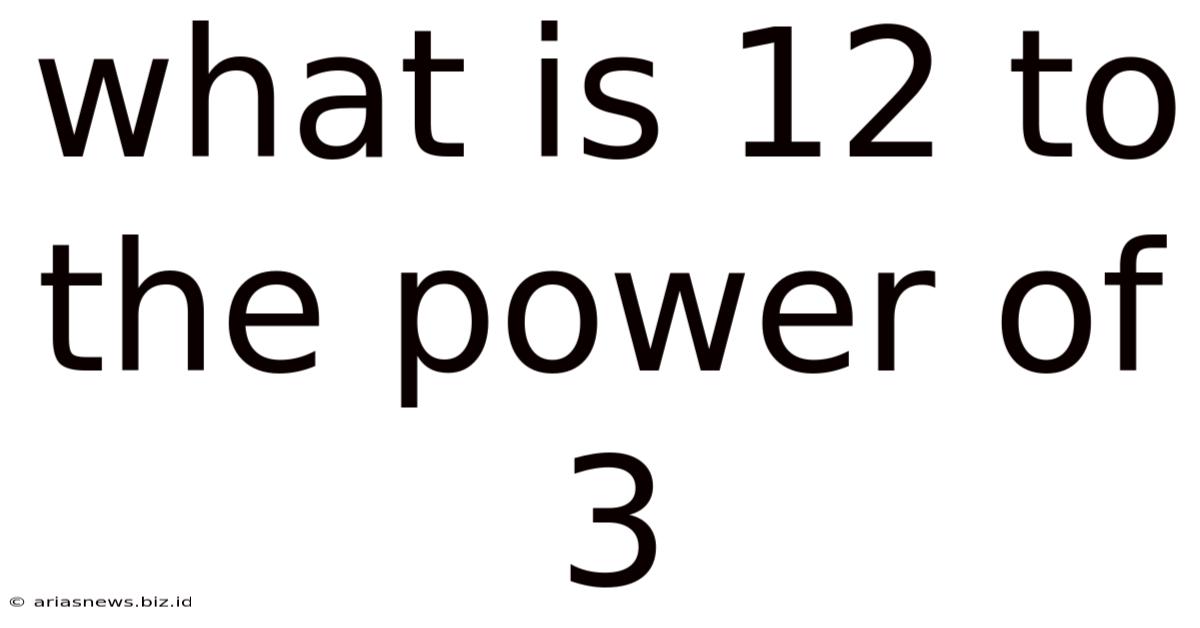
Table of Contents
What is 12 to the Power of 3? A Deep Dive into Exponentiation
Calculating 12 to the power of 3, or 12³, might seem like a simple mathematical problem. However, understanding the concept of exponentiation and its applications extends far beyond this single calculation. This article delves into the intricacies of exponents, exploring their meaning, practical applications, and the specific solution to 12³. We'll also touch upon related mathematical concepts and provide examples to solidify your understanding.
Understanding Exponentiation: The Power of Repeated Multiplication
Exponentiation, at its core, is repeated multiplication. When you see a number raised to a power (an exponent), it signifies that number being multiplied by itself a specific number of times. The base number is the number being multiplied, and the exponent indicates how many times it's multiplied. In our case, 12³ means 12 multiplied by itself three times: 12 x 12 x 12.
The Components of Exponentiation: Base and Exponent
- Base: The base is the number that is being raised to a power. In 12³, the base is 12.
- Exponent: The exponent, also known as the power or index, indicates how many times the base is multiplied by itself. In 12³, the exponent is 3.
Visualizing Exponentiation: From Repeated Multiplication to Geometric Representation
While we can easily perform the calculation 12 x 12 x 12, visualizing exponentiation can enhance understanding. Imagine a cube with sides of length 12 units. The volume of this cube would be 12 x 12 x 12 cubic units, directly representing 12³. This geometric interpretation provides a concrete visual representation of the abstract concept of exponentiation.
Calculating 12 to the Power of 3: The Step-by-Step Solution
Now, let's calculate 12³ step-by-step:
- First Multiplication: 12 x 12 = 144
- Second Multiplication: 144 x 12 = 1728
Therefore, 12³ = 1728.
Using Calculators and Software: Streamlining the Process
For larger numbers or more complex exponents, using a calculator or mathematical software is highly recommended. Most calculators have an exponent function (usually represented by a "^" or "x<sup>y</sup>" symbol) that simplifies the process. Simply input the base (12), the exponent (3), and the calculator will instantly provide the result: 1728.
Beyond 12³: Exploring Different Exponents and Bases
Understanding 12³ is a stepping stone to grasping the broader concept of exponentiation. Let's explore some variations:
Exponents Greater Than 3
Imagine calculating 12⁴ (12 to the power of 4). This would involve multiplying 12 by itself four times: 12 x 12 x 12 x 12 = 20736. As the exponent increases, the result grows exponentially larger.
Exponents of 0 and 1
- Exponent of 0: Any number (except 0) raised to the power of 0 equals 1. Therefore, 12⁰ = 1.
- Exponent of 1: Any number raised to the power of 1 equals itself. Therefore, 12¹ = 12.
Negative Exponents
Negative exponents represent reciprocals. For example, 12⁻² is the same as 1/(12²), which equals 1/144. The negative exponent indicates taking the reciprocal of the base raised to the positive exponent.
Fractional Exponents
Fractional exponents involve roots. For example, 12^(1/2) is the square root of 12, and 12^(1/3) is the cube root of 12. These introduce a whole new layer of mathematical complexity and are a great area for further exploration.
Real-World Applications of Exponentiation
Exponentiation isn't just a theoretical concept; it has numerous real-world applications across various fields:
Finance and Compound Interest
Compound interest calculations rely heavily on exponentiation. The formula for compound interest involves raising the principal amount plus the interest rate to the power of the number of compounding periods. This shows how your savings grow over time.
Science and Engineering
Exponential growth and decay are fundamental concepts in many scientific fields. Population growth, radioactive decay, and the spread of diseases often follow exponential patterns. Understanding exponentiation is crucial for modeling and predicting these phenomena.
Computer Science and Data Structures
Exponentiation plays a vital role in algorithms and data structures. The time complexity of some algorithms, such as binary search, is expressed using exponential notation. Understanding this helps determine the efficiency of algorithms.
Physics and Engineering
Many physical phenomena, such as the intensity of light or sound, decay exponentially with distance. Calculating these decay rates uses exponentiation.
Expanding Your Knowledge: Further Exploration of Related Mathematical Concepts
Understanding 12³ opens doors to exploring more complex mathematical concepts:
Logarithms
Logarithms are the inverse operation of exponentiation. If you have an equation like 12³ = 1728, the logarithm base 12 of 1728 is 3. Logarithms are essential for solving exponential equations and have wide applications in various fields.
Polynomial Functions
Polynomial functions involve terms with variables raised to various powers. Understanding exponents is crucial for working with these functions, which are used extensively in mathematics, science, and engineering to model various real-world phenomena.
Calculus
Calculus, a branch of mathematics dealing with continuous change, utilizes exponents extensively in concepts like derivatives and integrals. These concepts are crucial for understanding rates of change and accumulation.
Conclusion: Mastering Exponentiation and its Applications
While the calculation of 12³ might appear simple, it's a gateway to understanding the vast and powerful concept of exponentiation. From finance to science to computer science, this fundamental mathematical operation underpins numerous critical applications. By exploring the concept thoroughly, you gain a powerful tool for tackling complex problems and deepening your understanding of the world around us. Remember, understanding the "why" behind the calculation is as important as knowing the answer itself. This understanding lays the groundwork for tackling more advanced mathematical challenges and appreciating the elegance and power of mathematics in solving real-world problems. So, remember that 12³ = 1728, but also remember the broader context and the myriad of applications this seemingly simple calculation encompasses.
Latest Posts
Latest Posts
-
After Which Problem Solving Stage Should You Take Action
May 11, 2025
-
Is The Square Root Of 19 A Rational Number
May 11, 2025
-
What Do You Call A Male Cougar
May 11, 2025
-
In The Lorax What Does Unless Mean
May 11, 2025
-
Jeddah Kingdom Of Saudi Arabia Zip Code
May 11, 2025
Related Post
Thank you for visiting our website which covers about What Is 12 To The Power Of 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.