What Is 2 3 Cup Times 3
Arias News
May 12, 2025 · 5 min read
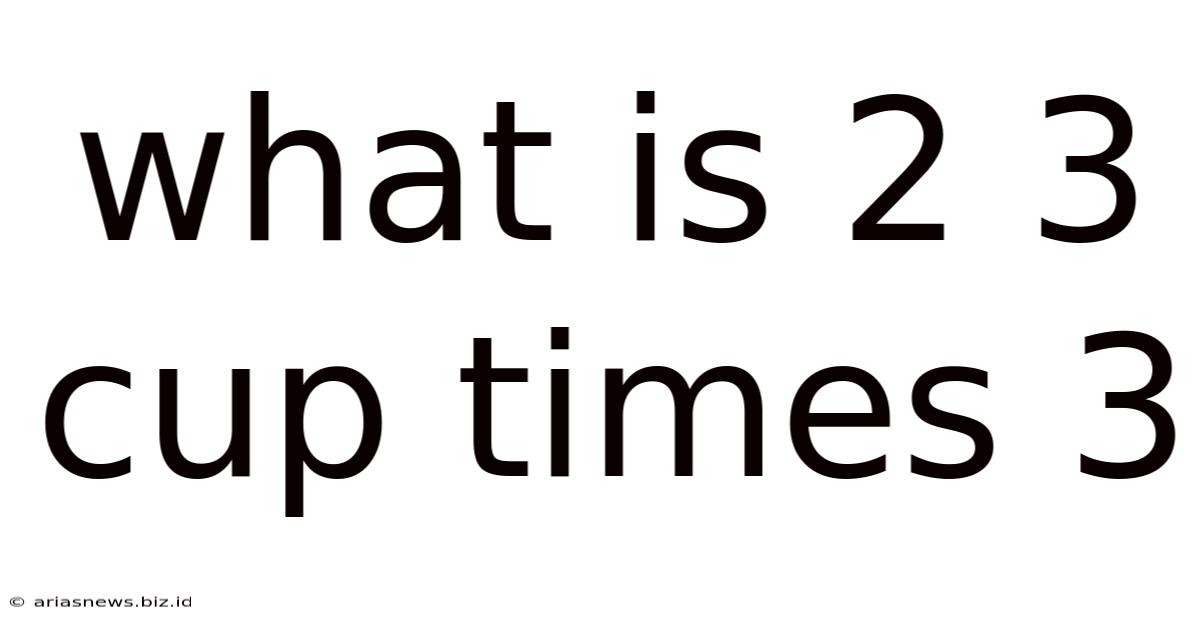
Table of Contents
What is 2 ⅓ Cups Times 3? A Deep Dive into Fraction Multiplication and Real-World Applications
This seemingly simple question, "What is 2 ⅓ cups times 3?", opens a door to a fundamental mathematical concept: fraction multiplication. While the answer might seem straightforward at first glance, exploring the different methods of solving it reveals valuable insights into working with fractions, a skill crucial in various aspects of life, from baking to construction to scientific calculations. This article will not only answer the question but also delve into the underlying principles, explore alternative approaches, and showcase practical applications of this type of calculation.
Understanding the Problem: 2 ⅓ Cups x 3
The problem presents a multiplication of a mixed number (2 ⅓) by a whole number (3). Before diving into the calculation, let's break down the components:
-
2 ⅓ cups: This represents a quantity measured in cups. The "2" represents two whole cups, and "⅓" represents one-third of a cup. This is a mixed number, combining a whole number and a fraction.
-
x 3: This indicates we need to triple the quantity of 2 ⅓ cups. We're essentially adding 2 ⅓ cups three times.
Method 1: Converting to an Improper Fraction
This is arguably the most common and efficient method for multiplying mixed numbers. The process involves:
1. Convert the Mixed Number to an Improper Fraction
A mixed number (a whole number and a fraction) can be converted to an improper fraction (where the numerator is larger than the denominator). To do this, we follow these steps:
- Multiply the whole number by the denominator: 2 x 3 = 6
- Add the numerator: 6 + 1 = 7
- Keep the same denominator: 3
Therefore, 2 ⅓ cups becomes the improper fraction ⁷⁄₃ cups.
2. Perform the Multiplication
Now we multiply the improper fraction by 3:
(⁷⁄₃) x 3 = ⁷⁄₃ x ³⁄₁ = 21⁄3
3. Simplify the Result
The resulting improper fraction (21⁄3) can be simplified to a whole number or a mixed number:
21 ÷ 3 = 7
Therefore, 2 ⅓ cups times 3 equals 7 cups.
Method 2: Distributive Property
The distributive property allows us to break down the multiplication into smaller, more manageable parts. We can think of 2 ⅓ cups as (2 cups + ⅓ cup). Then we multiply each part by 3:
(2 cups + ⅓ cup) x 3 = (2 cups x 3) + (⅓ cup x 3) = 6 cups + 1 cup = 7 cups
This method provides a more intuitive understanding of the multiplication process, particularly for those who find improper fractions challenging.
Method 3: Visual Representation
For a visual learner, a diagram can be helpful. Imagine three containers, each holding 2 ⅓ cups of a substance. Visually adding the amounts together clarifies the result:
[Insert a diagram here showing three containers, each with 2 full cups and one-third of a cup. The total should visually add up to 7 cups.]
Real-World Applications of Fraction Multiplication
Understanding fraction multiplication extends far beyond simple math problems. It's a vital skill in many areas:
1. Cooking and Baking
Recipes often require fractional measurements. Scaling up or down a recipe necessitates multiplying fractional quantities. For instance, if a recipe calls for 2 ⅓ cups of flour and you want to triple the recipe, you'll need to perform this exact calculation.
2. Construction and Engineering
Precise measurements are crucial in construction and engineering. Calculating material quantities, determining angles, and working with blueprints often involves multiplying fractions and mixed numbers.
3. Finance and Budgeting
Managing finances involves calculating percentages, interest rates, and portions of budgets. These calculations frequently require working with fractions.
4. Science and Medicine
Many scientific formulas and medical dosages involve fractions and ratios. Accurate calculations are essential for experimental accuracy and patient safety.
5. Sewing and Tailoring
Pattern adjustments and fabric calculations in sewing and tailoring often require precise measurements, making fraction multiplication essential for accurate results.
Beyond the Basics: More Complex Fraction Multiplication
While the initial problem was relatively straightforward, the principles involved can be applied to more complex scenarios:
-
Multiplying mixed numbers by mixed numbers: This involves converting both mixed numbers into improper fractions before multiplication, and then simplifying the result.
-
Multiplying fractions by decimals: This requires converting either the fraction or the decimal to a common form (either both to fractions or both to decimals) before multiplication.
-
Working with multiple fractions: Multiplying three or more fractions involves multiplying the numerators together and the denominators together, then simplifying the result.
Mastering Fraction Multiplication: Tips and Tricks
-
Practice Regularly: The key to mastering any mathematical skill is consistent practice. Start with simple problems and gradually increase the complexity.
-
Use Visual Aids: Diagrams, charts, and other visual aids can make understanding fraction multiplication easier.
-
Break Down Complex Problems: Divide complex problems into smaller, more manageable steps.
-
Check Your Work: Always check your calculations to ensure accuracy.
-
Utilize Online Resources: Numerous online resources, including calculators and tutorials, can provide assistance and extra practice.
Conclusion: The Significance of Fraction Multiplication in Everyday Life
The seemingly simple question, "What is 2 ⅓ cups times 3?", unveils the importance of fraction multiplication in our daily lives. From baking a cake to constructing a building, understanding how to work with fractions is crucial for accuracy and efficiency. Mastering this fundamental skill empowers us to tackle more complex mathematical challenges and successfully navigate various aspects of our world. By understanding the different methods and practicing regularly, we can confidently conquer any fraction multiplication problem we encounter. This article has hopefully provided a comprehensive guide to this crucial mathematical concept, equipped you with different approaches, and demonstrated its practical relevance across numerous fields. Remember, the more you practice, the more proficient you’ll become!
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is 2 3 Cup Times 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.