What Is 20/25 As A Percentage
Arias News
May 20, 2025 · 4 min read
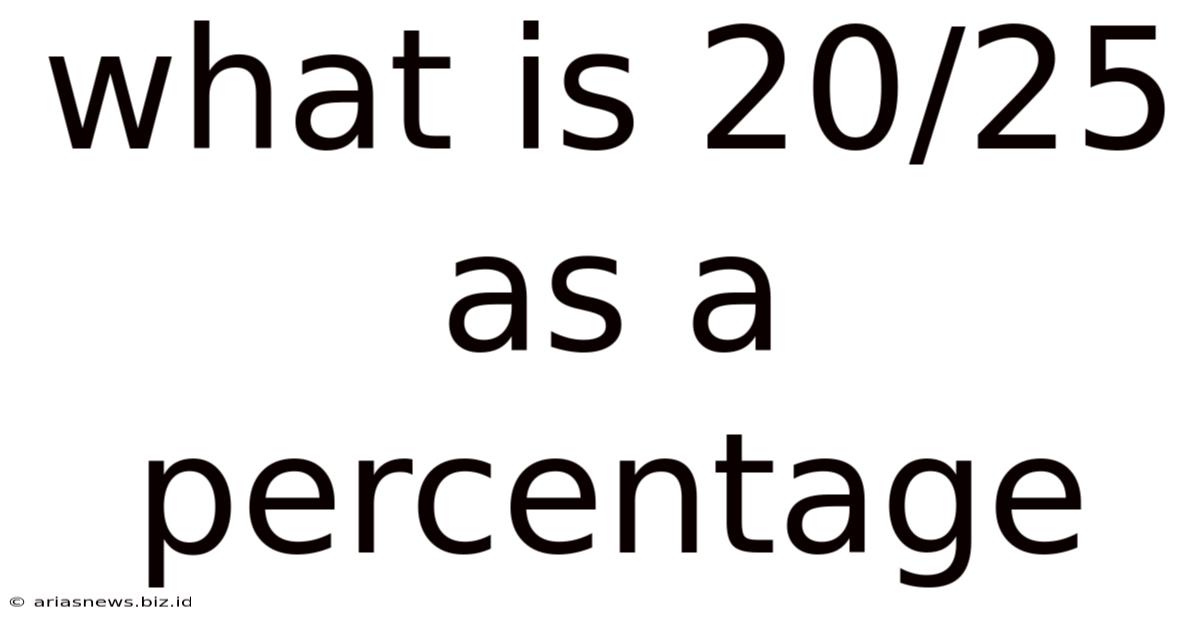
Table of Contents
What is 20/25 as a Percentage? A Comprehensive Guide
Converting fractions to percentages is a fundamental skill in mathematics with wide-ranging applications in everyday life, from calculating discounts in shopping to understanding financial reports. This comprehensive guide will delve into the process of converting the fraction 20/25 into a percentage, exploring various methods and providing a deeper understanding of the underlying concepts. We'll also discuss the practical implications and applications of this conversion.
Understanding Fractions and Percentages
Before we tackle the conversion of 20/25, let's clarify the basics of fractions and percentages.
Fractions: A fraction represents a part of a whole. It consists of two numbers: the numerator (the top number) and the denominator (the bottom number). The numerator indicates how many parts we have, and the denominator indicates the total number of parts the whole is divided into. In our case, 20/25 means we have 20 parts out of a total of 25 parts.
Percentages: A percentage is a way of expressing a number as a fraction of 100. The symbol "%" represents "per cent," which literally means "out of one hundred." Percentages are incredibly useful for comparing proportions and making sense of data in various contexts.
Method 1: Simplifying the Fraction
The simplest way to convert 20/25 to a percentage involves first simplifying the fraction. Simplifying a fraction means reducing it to its lowest terms by dividing both the numerator and denominator by their greatest common divisor (GCD).
In this case, the GCD of 20 and 25 is 5. Dividing both the numerator and denominator by 5, we get:
20 ÷ 5 = 4 25 ÷ 5 = 5
Therefore, 20/25 simplifies to 4/5.
Method 2: Converting the Simplified Fraction to a Percentage
Now that we have the simplified fraction 4/5, we can easily convert it to a percentage. To do this, we need to express the fraction as an equivalent fraction with a denominator of 100.
We can set up a proportion:
4/5 = x/100
To solve for x (the numerator of the equivalent fraction with a denominator of 100), we can cross-multiply:
4 * 100 = 5 * x 400 = 5x x = 400 ÷ 5 x = 80
Therefore, 4/5 is equal to 80/100, which is equivalent to 80%.
Method 3: Direct Conversion Using Decimal
Another approach is to first convert the fraction to a decimal and then multiply by 100 to get the percentage.
- Convert the fraction to a decimal: Divide the numerator (20) by the denominator (25):
20 ÷ 25 = 0.8
- Multiply the decimal by 100:
0.8 * 100 = 80
Therefore, 20/25 is equal to 80%.
Practical Applications of Percentage Conversions
Understanding how to convert fractions to percentages has numerous practical applications across various fields:
- Finance: Calculating interest rates, discounts, profits, and losses. For example, if a store offers a 20% discount on an item, you can use this knowledge to determine the actual price.
- Statistics: Representing data in a more understandable and comparable way. Percentages are frequently used in graphs, charts, and reports to visualize data proportions.
- Science: Expressing experimental results and probabilities. For instance, calculating the percentage yield in a chemical reaction.
- Everyday Life: Calculating tips in restaurants, understanding sales tax, or determining the percentage of completion of a task.
Further Exploration: Working with Different Fractions
The methods outlined above can be applied to convert any fraction to a percentage. Let's consider a few examples:
- Converting 1/4 to a percentage: 1/4 = 25/100 = 25%
- Converting 3/8 to a percentage: 3/8 = 0.375 = 37.5%
- Converting 7/10 to a percentage: 7/10 = 70/100 = 70%
Troubleshooting Common Errors
When converting fractions to percentages, some common errors can occur:
- Incorrect simplification of the fraction: Always ensure you simplify the fraction to its lowest terms before converting to a percentage. This will make the calculation easier and prevent inaccuracies.
- Errors in decimal-to-percentage conversion: Remember to multiply the decimal by 100 to obtain the percentage.
- Misunderstanding the concept of percentages: A solid understanding of what a percentage represents is crucial for accurate conversions and interpretation of results.
Conclusion: Mastering Percentage Conversions
Converting fractions to percentages is a valuable skill with broad applications. By understanding the different methods and practicing regularly, you can improve your proficiency in this area. Whether you're dealing with financial calculations, statistical analysis, or everyday problems, the ability to confidently convert fractions to percentages will enhance your problem-solving skills and make you more comfortable working with numerical data. Remember the key steps: simplify the fraction (if possible), convert to a decimal, and then multiply by 100 to find the percentage. Practice makes perfect, so keep working through examples to reinforce your understanding and build your confidence. This will not only improve your mathematical abilities but also equip you to tackle real-world problems effectively.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is 20/25 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.