What Is 26 Out Of 30 As A Percentage
Arias News
May 08, 2025 · 5 min read
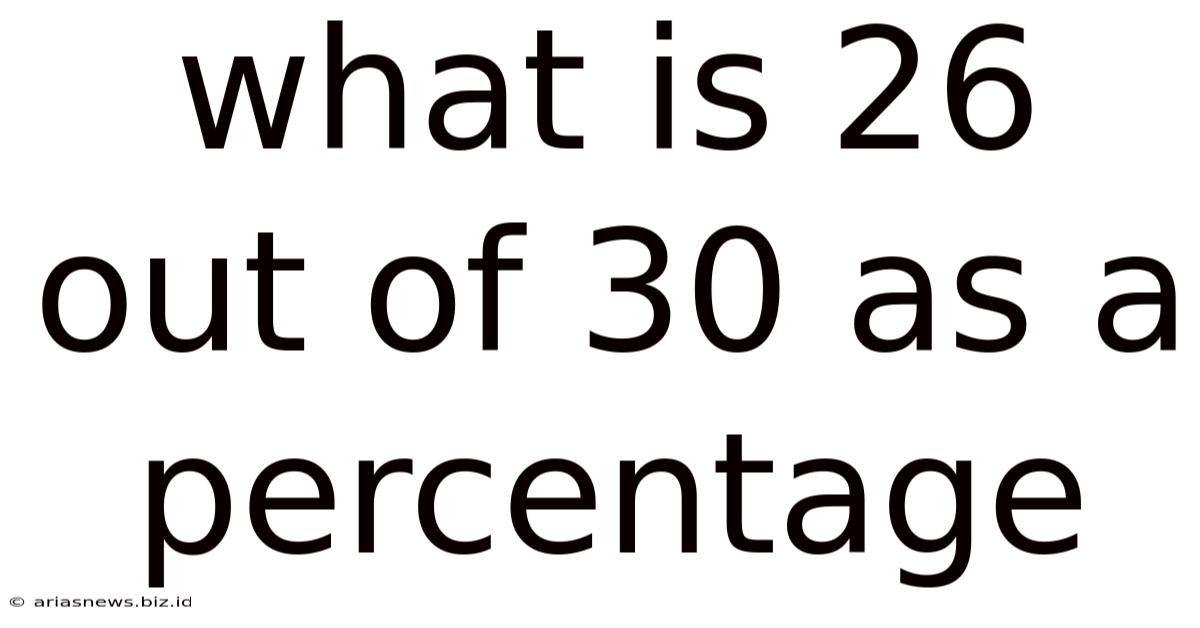
Table of Contents
What is 26 out of 30 as a Percentage? A Comprehensive Guide
Calculating percentages is a fundamental skill applicable across numerous fields, from everyday budgeting to complex scientific analyses. Understanding how to convert fractions to percentages is crucial for interpreting data, making comparisons, and presenting information effectively. This comprehensive guide delves into the calculation of "26 out of 30 as a percentage," explaining the method, providing variations, and exploring practical applications.
Understanding Percentages
Before we delve into the specific calculation, let's refresh our understanding of percentages. A percentage represents a fraction of 100. The word "percent" itself derives from the Latin "per centum," meaning "out of one hundred." Therefore, 50% means 50 out of 100, or 50/100, which simplifies to 1/2.
Calculating 26 out of 30 as a Percentage: The Basic Method
The most straightforward method involves converting the fraction 26/30 into a percentage. Here's a step-by-step breakdown:
-
Set up the fraction: Express the problem as a fraction: 26/30. This represents 26 parts out of a total of 30 parts.
-
Convert the fraction to a decimal: Divide the numerator (26) by the denominator (30): 26 ÷ 30 = 0.866666... The result is a recurring decimal.
-
Convert the decimal to a percentage: Multiply the decimal by 100: 0.866666... × 100 = 86.6666...%
-
Round to the desired precision: Depending on the level of accuracy needed, round the percentage. Rounding to two decimal places, we get 86.67%.
Therefore, 26 out of 30 is 86.67%.
Alternative Methods for Calculation
While the basic method is perfectly adequate, alternative methods can be useful depending on the context and the tools available.
Using a Calculator:
Most calculators have a percentage function. Simply input 26 ÷ 30 and then multiply by 100. The calculator will directly provide the percentage. This is the quickest and often most accurate method, especially for complex calculations.
Using Proportions:
This method is particularly helpful for understanding the underlying concept. Set up a proportion:
26/30 = x/100
Cross-multiply: 30x = 2600
Solve for x: x = 2600/30 = 86.67
This method clearly demonstrates the relationship between the fraction and the percentage.
Using Spreadsheet Software:
Spreadsheet software like Microsoft Excel or Google Sheets has built-in functions to calculate percentages. For example, in Excel, you could use the formula =26/30*100 or the PERCENTAGE function. These are efficient for larger datasets or when performing repeated calculations.
Practical Applications: Real-World Examples
Understanding percentage calculations is essential in numerous real-world scenarios:
Academic Performance:
Imagine a student scores 26 out of 30 on a test. Knowing that this equates to 86.67% allows for easy comparison with other students' scores and assessment of their overall performance. This is crucial for teachers, students, and parents in understanding academic progress.
Business and Finance:
In business, percentages are ubiquitous. Calculating profit margins, sales growth, market share, and discount rates all involve percentage calculations. For instance, a company might see a 26% increase in sales over the previous year, representing a significant growth metric.
Data Analysis and Statistics:
In statistical analysis, percentages are used to represent proportions within a data set. This could be used to analyze survey results, customer demographics, or market research findings. For example, a survey might find that 26 out of 30 respondents prefer a specific product, highlighting the product's popularity.
Everyday Life:
Percentages are used in many everyday contexts, such as calculating tips in restaurants (e.g., a 15% tip on a $30 meal), understanding discounts in shops (e.g., a 20% discount on a $50 item), and monitoring personal finances (e.g., calculating savings rate or debt reduction progress).
Beyond the Basics: Understanding the Significance of Precision
While we rounded the percentage to 86.67%, the true value is a recurring decimal (86.666...). The level of precision required depends on the context. For casual calculations, two decimal places usually suffice. However, in scientific or financial applications, greater accuracy may be necessary. Using more decimal places provides a more precise representation of the data, which is crucial for accurate analyses and comparisons.
Error Handling and Avoiding Common Mistakes
Even seemingly simple percentage calculations can be prone to errors. Here are some common mistakes to watch out for:
- Incorrect order of operations: Always perform the division before multiplying by 100.
- Rounding errors: Be mindful of the implications of rounding, especially when performing multiple calculations involving percentages. Rounding early can lead to significant inaccuracies in the final result.
- Misunderstanding the context: Ensure you understand what the numerator and denominator represent in the context of the problem.
Expanding Your Knowledge: Further Exploration of Percentages
Understanding percentages forms the foundation for numerous advanced mathematical concepts, including:
- Compound interest: Calculating interest earned on both principal and accumulated interest.
- Statistical analysis: Analyzing data distributions and making inferences using percentages and proportions.
- Financial modeling: Building financial models to predict future outcomes based on percentage changes and growth rates.
By mastering the basic principles of percentage calculations, you unlock the ability to understand and interpret information across various domains.
Conclusion: Mastering the Art of Percentage Calculations
Calculating "26 out of 30 as a percentage" is a straightforward process, yielding a result of 86.67%. However, this simple calculation highlights the fundamental importance of understanding percentages in everyday life, academic pursuits, and professional settings. By understanding the different methods of calculation, their practical applications, and common pitfalls, you equip yourself with a valuable skill for interpreting data, making informed decisions, and effectively communicating quantitative information. Remember to choose the method most suitable for the context and prioritize accuracy to avoid misleading conclusions.
Latest Posts
Latest Posts
-
What Is The Highest Common Factor Of 24 And 32
May 08, 2025
-
How Many Cups Are In A Pound Of Noodles
May 08, 2025
-
Is Andy Mill Still Married To Debra Harvick
May 08, 2025
-
How Many Words Can You Make Out Of Halloween
May 08, 2025
-
How Much Is One Gallon In Litres
May 08, 2025
Related Post
Thank you for visiting our website which covers about What Is 26 Out Of 30 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.