What Is 3 8 Divided By 1 4
Arias News
May 11, 2025 · 5 min read
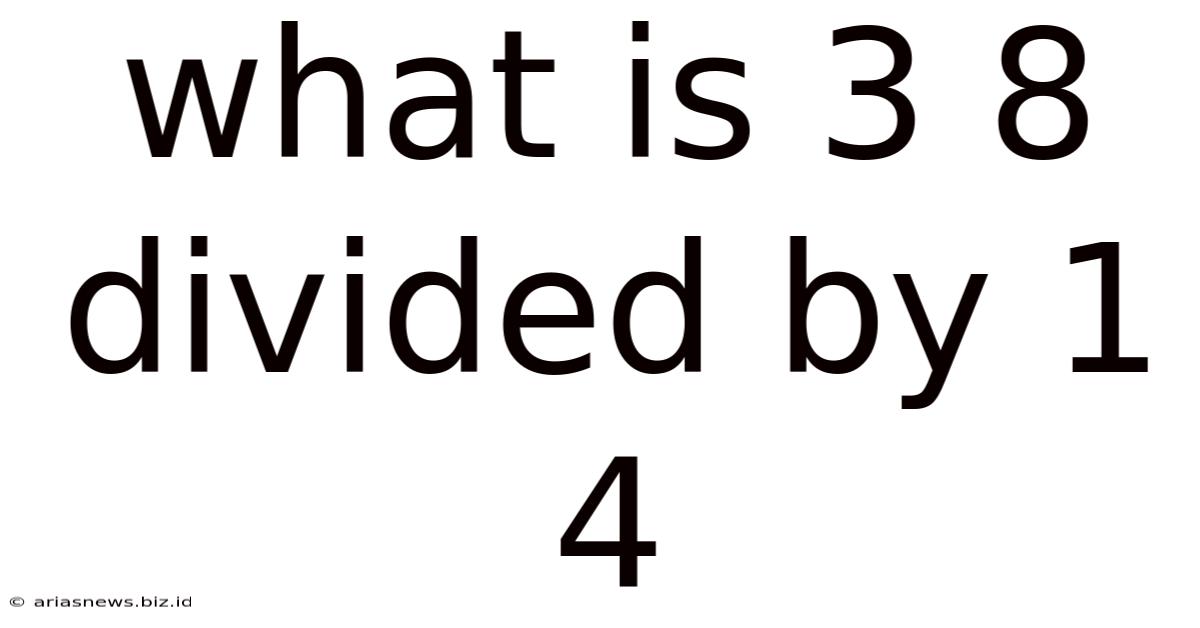
Table of Contents
What is 3/8 Divided by 1/4? A Comprehensive Guide to Fraction Division
Understanding fraction division can seem daunting at first, but with a clear, step-by-step approach, it becomes manageable and even enjoyable. This comprehensive guide will not only solve the problem "What is 3/8 divided by 1/4?" but will also equip you with the knowledge and skills to tackle any fraction division problem with confidence. We’ll explore the underlying concepts, delve into various solution methods, and even touch upon real-world applications of this essential mathematical skill.
Understanding Fractions and Division
Before diving into the specific problem, let's refresh our understanding of fractions and division. A fraction represents a part of a whole. It's composed of a numerator (the top number) and a denominator (the bottom number). The numerator indicates how many parts we have, and the denominator indicates how many equal parts the whole is divided into.
Division, in its simplest form, is about finding out how many times one number (the divisor) goes into another number (the dividend). When dealing with fractions, this concept remains the same, although the process might appear slightly different.
Method 1: The "Keep, Change, Flip" Method (or Invert and Multiply)
This is arguably the most popular and easiest method for dividing fractions. It involves three simple steps:
1. Keep: Keep the first fraction (the dividend) exactly as it is. In our case, this is 3/8.
2. Change: Change the division sign (÷) to a multiplication sign (×).
3. Flip: Flip the second fraction (the divisor) – this means swapping the numerator and the denominator. The reciprocal of 1/4 is 4/1.
Therefore, the problem "3/8 divided by 1/4" transforms into:
3/8 × 4/1
Now, we simply multiply the numerators together and the denominators together:
(3 × 4) / (8 × 1) = 12/8
This fraction can be simplified by dividing both the numerator and the denominator by their greatest common divisor (GCD), which is 4:
12/8 = (12 ÷ 4) / (8 ÷ 4) = 3/2
This improper fraction can be converted to a mixed number:
3/2 = 1 ½
Therefore, 3/8 divided by 1/4 is equal to 1 ½ or 1.5.
Method 2: Using Complex Fractions
Another way to approach fraction division is by using complex fractions. A complex fraction is a fraction where the numerator, the denominator, or both contain fractions. We can represent our problem as a complex fraction:
(3/8) / (1/4)
To solve this, we multiply the numerator by the reciprocal of the denominator:
(3/8) × (4/1) = 12/8 = 3/2 = 1 ½
This method arrives at the same answer as the "Keep, Change, Flip" method, demonstrating the equivalence of the two approaches.
Method 3: Finding a Common Denominator
While less common for dividing fractions, using a common denominator is a valid approach. This method is more intuitive for those who prefer a visual understanding.
1. Find a common denominator: The least common multiple (LCM) of 8 and 4 is 8.
2. Convert fractions to equivalent fractions with the common denominator:
3/8 remains as 3/8.
1/4 becomes 2/8 (multiply both numerator and denominator by 2).
3. Rewrite the division problem:
(3/8) / (2/8)
4. Divide the numerators:
3 ÷ 2 = 1.5
This method yields the same result: 1 ½ or 1.5.
Real-World Applications of Fraction Division
Fraction division isn't just a theoretical concept; it has numerous practical applications in everyday life:
-
Cooking and Baking: Scaling recipes up or down often involves dividing fractions. For instance, if a recipe calls for 1/4 cup of sugar and you want to make half the recipe, you need to divide 1/4 by 2.
-
Sewing and Crafts: Calculating fabric requirements or dividing lengths of yarn frequently requires fraction division.
-
Construction and Carpentry: Dividing lumber, measuring distances, and calculating angles often involve fractions.
-
Data Analysis: When working with datasets involving proportions or percentages, you'll often encounter fraction division.
-
Finance: Calculating shares of profits, splitting bills, or understanding interest rates often involves working with fractions.
Further Exploration: Dividing Fractions with Mixed Numbers
Let's expand our understanding by tackling problems involving mixed numbers. A mixed number combines a whole number and a fraction (e.g., 1 ½). To divide fractions involving mixed numbers, you first need to convert the mixed numbers into improper fractions.
For example, let's solve 1 ½ divided by ¼:
1. Convert mixed numbers to improper fractions:
1 ½ = (1 × 2 + 1) / 2 = 3/2
2. Apply the "Keep, Change, Flip" method:
(3/2) ÷ (1/4) becomes (3/2) × (4/1) = 12/2 = 6
Therefore, 1 ½ divided by ¼ is equal to 6.
Troubleshooting Common Mistakes
Several common errors can occur when dividing fractions. Here's how to avoid them:
-
Flipping the wrong fraction: Remember, only the divisor (the second fraction) is flipped.
-
Incorrect multiplication: Double-check your multiplication of numerators and denominators.
-
Forgetting to simplify: Always simplify your final answer to its lowest terms.
-
Improper conversion of mixed numbers: Ensure you correctly convert mixed numbers to improper fractions before performing the division.
Conclusion: Mastering Fraction Division
Dividing fractions might seem intimidating initially, but with consistent practice and a clear understanding of the underlying principles, it becomes a straightforward process. By mastering the "Keep, Change, Flip" method, utilizing complex fractions, or employing the common denominator approach, you can confidently tackle any fraction division problem. Remember to practice regularly, apply the concepts to real-world scenarios, and don't hesitate to review the steps whenever needed. With dedication and practice, you'll become proficient in fraction division and unlock a new level of mathematical understanding. The solution to "What is 3/8 divided by 1/4?" is definitively 1 ½, and you now have the tools to solve countless other fraction division problems with ease.
Latest Posts
Latest Posts
-
How Many Centimeters Are In 3 5 Meters
May 12, 2025
-
Can You Eat Cream Cheese Past The Expiration Date
May 12, 2025
-
Does Coffee Lose Its Caffeine Over Time
May 12, 2025
-
A Typical Number For A Contra Account Would Be
May 12, 2025
-
Are Chili Flakes And Red Pepper Flakes The Same Thing
May 12, 2025
Related Post
Thank you for visiting our website which covers about What Is 3 8 Divided By 1 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.