What Is 3 To The Fifth Power
Arias News
Apr 03, 2025 · 5 min read
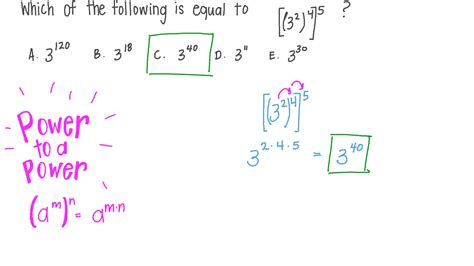
Table of Contents
What is 3 to the Fifth Power? A Comprehensive Exploration
The seemingly simple question, "What is 3 to the fifth power?" opens a door to a fascinating world of mathematics, encompassing exponentiation, its applications, and its broader significance within the field of numbers. This article will delve deep into understanding this specific calculation, exploring its underlying principles and expanding upon its relevance in various mathematical contexts.
Understanding Exponentiation: The Foundation of 3 to the Fifth Power
Before we calculate 3 to the fifth power (often written as 3⁵), let's establish a firm understanding of exponentiation. Exponentiation is a mathematical operation that involves raising a base number to a certain power (or exponent). It signifies repeated multiplication of the base number by itself. The general form is represented as: b<sup>n</sup>, where 'b' is the base and 'n' is the exponent. This means multiplying 'b' by itself 'n' times.
For example:
- 2² (2 to the power of 2, or 2 squared) = 2 x 2 = 4
- 5³ (5 to the power of 3, or 5 cubed) = 5 x 5 x 5 = 125
- 10⁴ (10 to the power of 4) = 10 x 10 x 10 x 10 = 10,000
Calculating 3 to the Fifth Power
Now, let's tackle the central question: What is 3 to the fifth power (3⁵)? Following the definition of exponentiation, we perform the following calculation:
3⁵ = 3 x 3 x 3 x 3 x 3 = 243
Therefore, 3 to the fifth power equals 243. This seemingly simple calculation forms the basis for understanding more complex mathematical operations and concepts.
Expanding the Understanding: Beyond the Calculation
The calculation itself is straightforward, but the implications and applications of exponentiation, as demonstrated by 3⁵, are far-reaching. Let's explore some of them:
1. Exponential Growth and Decay
Exponentiation is fundamental to understanding exponential growth and decay. These are processes where a quantity increases or decreases at a rate proportional to its current value. Examples include:
- Population Growth: If a population increases by a fixed percentage each year, its growth follows an exponential pattern.
- Compound Interest: The interest earned on savings accounts or investments often compounds, meaning interest is earned on both the principal and accumulated interest. This leads to exponential growth of the investment.
- Radioactive Decay: The decay rate of radioactive materials is exponential, with the amount of remaining material decreasing by a constant percentage over time.
2. Scientific Notation and Large Numbers
Exponentiation is crucial for representing extremely large or extremely small numbers in scientific notation. Scientific notation uses powers of 10 to express numbers concisely. For instance, the speed of light is approximately 3 x 10⁸ meters per second. This notation makes it far easier to handle numbers with many digits. Understanding 3⁵ lays a groundwork for grasping and manipulating numbers expressed in scientific notation.
3. Polynomial Equations and Algebra
Exponentiation plays a significant role in algebra, particularly in polynomial equations. Polynomials are expressions involving variables raised to various powers. Solving polynomial equations often involves manipulating terms involving exponentiation. Understanding the concept of exponents is crucial for tackling more advanced algebraic problems.
For example, consider the polynomial equation: x⁵ - 243 = 0. Solving this equation involves finding the value of 'x' that satisfies the equation. The solution, in this case, is directly related to our understanding of 3⁵.
4. Computer Science and Algorithms
Exponentiation is a core operation in computer science and algorithm design. Many algorithms rely on repeated operations, and exponentiation provides a concise way to represent these operations. For instance, algorithms related to cryptography often utilize exponentiation for encryption and decryption processes.
5. Geometry and Measurement
Exponentiation also appears in geometric calculations, particularly in determining volumes and areas of three-dimensional shapes. For example, the volume of a cube is calculated as side³, highlighting the application of exponents in geometric measurements.
Beyond 3⁵: Exploring Other Exponents and Bases
While this article focuses on 3⁵, it's important to understand that exponentiation applies to a wide range of bases and exponents. Let's briefly explore some related concepts:
- Negative Exponents: A negative exponent indicates the reciprocal of the base raised to the positive exponent. For example, 3⁻² = 1/3² = 1/9.
- Fractional Exponents: Fractional exponents represent roots. For example, 8<sup>(1/3)</sup> represents the cube root of 8, which is 2.
- Zero Exponent: Any number (except zero) raised to the power of zero equals 1. For example, 3⁰ = 1.
Practical Applications and Real-World Examples
The concept of 3⁵, and exponentiation in general, has significant practical applications in various fields:
- Finance: Calculating compound interest, determining the future value of investments, and understanding loan amortization schedules all involve exponentiation.
- Physics: Many physical phenomena, such as radioactive decay, population growth, and the propagation of waves, are modeled using exponential functions.
- Engineering: Designing structures, calculating stresses and strains, and modeling dynamic systems often involves exponential calculations.
- Biology: Modeling population growth, bacterial growth, and the spread of diseases relies heavily on exponential functions.
- Computer Science: Hashing algorithms, cryptography, and data compression often make use of exponentiation.
Conclusion: The Significance of 3 to the Fifth Power
While the calculation of 3⁵ might seem simple on the surface (resulting in 243), its significance extends far beyond a single numerical answer. It represents a fundamental concept in mathematics – exponentiation – that underpins many complex calculations and models in diverse fields. Understanding 3⁵ provides a stepping stone to comprehending exponential growth, decay, and the broader applications of this vital mathematical operation across various disciplines. Its importance lies not just in the answer itself but in its foundational role in the wider mathematical landscape and its practical relevance to the real world. The seemingly simple 243 holds within it the key to understanding complex phenomena and solving intricate problems in a multitude of fields.
Latest Posts
Latest Posts
-
How Do You Say Ashley In Spanish
Apr 04, 2025
-
Distance From Tempe Az To Phoenix Az
Apr 04, 2025
-
What Does It Mean When A Bird Hits Your Windshield
Apr 04, 2025
-
How Long Does It Take To Walk 1 2 Miles
Apr 04, 2025
-
How Do You Say Panda Bear In Spanish
Apr 04, 2025
Related Post
Thank you for visiting our website which covers about What Is 3 To The Fifth Power . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
