What Is 3 To The Power Of 3
Arias News
Apr 01, 2025 · 4 min read
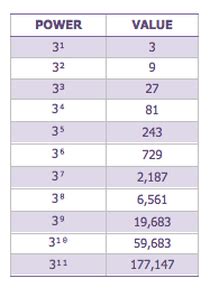
Table of Contents
What is 3 to the Power of 3? A Deep Dive into Exponentiation
The seemingly simple question, "What is 3 to the power of 3?" opens a door to a fascinating world of mathematics, specifically exponentiation. While the answer itself is straightforward (27), exploring the concept provides a deeper understanding of fundamental mathematical principles and their applications in various fields. This comprehensive guide will delve into the meaning of 3³, explore its applications, and touch upon related mathematical concepts.
Understanding Exponentiation: The Basics
Exponentiation, often represented as a base raised to an exponent (or power), signifies repeated multiplication. In the expression bⁿ, 'b' is the base, and 'n' is the exponent. This means 'b' is multiplied by itself 'n' times. For example:
- 2² = 2 x 2 = 4 (2 multiplied by itself twice)
- 5³ = 5 x 5 x 5 = 125 (5 multiplied by itself three times)
- 10⁴ = 10 x 10 x 10 x 10 = 10,000 (10 multiplied by itself four times)
Therefore, 3 to the power of 3, or 3³, represents 3 multiplied by itself three times: 3 x 3 x 3 = 27.
Why is Understanding Exponentiation Important?
Exponentiation is far more than a simple mathematical operation; it's a fundamental concept with wide-ranging applications across numerous disciplines:
-
Science: Exponential growth and decay are crucial in understanding phenomena like population growth (bacteria, human populations), radioactive decay, and compound interest. Understanding exponentiation allows scientists to model and predict these processes accurately.
-
Engineering: Many engineering calculations, particularly in fields like structural engineering and electrical engineering, rely heavily on exponentiation. For instance, calculating the strength of materials or analyzing electrical circuits often involves exponential equations.
-
Computer Science: Exponentiation is fundamental to computer algorithms and data structures. Concepts like binary numbers (base-2 exponentiation) are the building blocks of computer operation. The efficiency of algorithms is often analyzed using exponential functions (e.g., O(2ⁿ) complexity).
-
Finance: Compound interest calculations rely on exponential growth. Understanding exponentiation is crucial for anyone managing investments or loans.
Beyond 3³: Exploring Different Bases and Exponents
While we've focused on 3³, it's beneficial to broaden our perspective and consider other bases and exponents. This will solidify our understanding of exponentiation and its flexibility:
-
Different Bases: Let's consider different bases raised to the power of 3:
- 2³ = 2 x 2 x 2 = 8
- 4³ = 4 x 4 x 4 = 64
- 10³ = 10 x 10 x 10 = 1000
- 0.5³ = 0.5 x 0.5 x 0.5 = 0.125
-
Different Exponents: Now, let's keep the base as 3 but vary the exponent:
- 3¹ = 3
- 3² = 3 x 3 = 9
- 3³ = 3 x 3 x 3 = 27
- 3⁴ = 3 x 3 x 3 x 3 = 81
- 3⁵ = 3 x 3 x 3 x 3 x 3 = 243
Notice the pattern: as the exponent increases, the result grows exponentially.
Negative Exponents and Fractional Exponents
The concept of exponentiation extends beyond positive integer exponents. We can also explore:
-
Negative Exponents: A negative exponent signifies the reciprocal of the base raised to the positive exponent. For example:
- 3⁻¹ = 1/3
- 3⁻² = 1/3² = 1/9
- 3⁻³ = 1/3³ = 1/27
-
Fractional Exponents: Fractional exponents represent roots. For instance:
- 3^(1/2) = √3 (the square root of 3)
- 3^(1/3) = ³√3 (the cube root of 3)
- 3^(2/3) = (³√3)² (the square of the cube root of 3)
Applications of 3³ and Related Concepts in Real-World Scenarios
Let's illustrate how the concept of 3³ and related exponential concepts manifest in practical applications:
-
Volume Calculation: Imagine a cube with sides of 3 units each. The volume of this cube is 3³ = 27 cubic units. This simple calculation demonstrates the practical application of exponentiation in geometry.
-
Compound Interest: If you invest $1000 at an annual interest rate of 10%, compounded annually, after 3 years, the amount would be calculated using exponentiation. The formula would involve (1 + 0.1)³, showing the power of exponential growth in finance.
-
Growth of a Bacterial Colony: If a bacterial colony triples in size every hour, the size after 3 hours would be calculated using 3³. This illustrates exponential growth in biology.
Advanced Concepts and Related Topics
For a more in-depth understanding, exploring the following advanced concepts can prove invaluable:
-
Logarithms: Logarithms are the inverse of exponentiation. They help in solving equations where the variable is an exponent.
-
Exponential Functions: These functions are defined by expressions where the variable appears in the exponent (e.g., y = aˣ). They are crucial for modeling various phenomena exhibiting exponential growth or decay.
-
Taylor Series and Exponential Function: The exponential function, eˣ, can be represented using the Taylor series expansion, which provides a powerful tool for approximation and analysis.
Conclusion: The Significance of a Simple Calculation
The seemingly simple calculation of 3³ unveils a wealth of mathematical concepts and their pervasive applications in various fields. From understanding fundamental principles of exponentiation to appreciating its role in complex models and calculations, exploring this concept allows us to appreciate the depth and breadth of mathematics. This comprehensive guide hopefully provides a firm foundation for anyone interested in understanding exponentiation and its significance in the world around us. Further exploration of the concepts discussed here will only strengthen your understanding of these powerful mathematical tools.
Latest Posts
Latest Posts
-
How Far Away Can You See Fireworks At Night
Apr 02, 2025
-
How Much Is A Quarter Of 1 Million
Apr 02, 2025
-
How Many Ounces In 500 Ml Of Water
Apr 02, 2025
-
6pm To 6am Is How Many Hours
Apr 02, 2025
-
How Many Chicken Nuggets Is 4 Oz
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about What Is 3 To The Power Of 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
