What Is 3 To The Zeroth Power
Arias News
Mar 30, 2025 · 5 min read
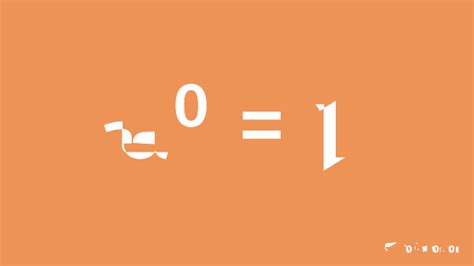
Table of Contents
What is 3 to the Zeroth Power? Unraveling the Mystery of Exponents
The question, "What is 3 to the zeroth power?" might seem deceptively simple. However, understanding this seemingly elementary concept unlocks a deeper appreciation of exponential notation and its fundamental role in mathematics, science, and even computer programming. This comprehensive guide will not only answer this question definitively but also delve into the underlying principles, explore practical applications, and address common misconceptions surrounding this mathematical quirk.
Understanding Exponents: A Foundation
Before tackling 3<sup>0</sup>, let's establish a solid understanding of exponents. Exponents, also known as powers or indices, represent repeated multiplication. For instance:
- 3<sup>2</sup> means 3 multiplied by itself twice: 3 * 3 = 9
- 3<sup>3</sup> means 3 multiplied by itself three times: 3 * 3 * 3 = 27
- 3<sup>4</sup> means 3 multiplied by itself four times: 3 * 3 * 3 * 3 = 81
Notice a pattern? As the exponent increases by one, we multiply by an additional factor of 3. This consistent pattern is key to understanding what happens when the exponent is zero.
The Curious Case of 3<sup>0</sup>: Why it Equals 1
The rule governing exponents states that any non-zero number raised to the power of zero equals 1. Therefore, 3<sup>0</sup> = 1. But why? Several approaches can help illustrate this seemingly counterintuitive result:
1. The Pattern Approach: A Consistent Descent
Let's examine a descending sequence of powers of 3:
- 3<sup>4</sup> = 81
- 3<sup>3</sup> = 27
- 3<sup>2</sup> = 9
- 3<sup>1</sup> = 3
Observe that each time the exponent decreases by 1, the result is divided by 3. Following this consistent pattern, to find 3<sup>0</sup>, we divide 3<sup>1</sup> by 3:
3 / 3 = 1
This pattern-based approach intuitively suggests that 3<sup>0</sup> must equal 1.
2. The Rule of Exponent Division: Maintaining Consistency
Another approach involves the rule of exponent division: When dividing exponential expressions with the same base, you subtract the exponents. Consider this example:
3<sup>2</sup> / 3<sup>2</sup> = 3<sup>(2-2)</sup> = 3<sup>0</sup>
However, any number divided by itself equals 1. Therefore:
3<sup>2</sup> / 3<sup>2</sup> = 9 / 9 = 1
This demonstrates that 3<sup>0</sup> must be equal to 1 to maintain consistency with the rules of exponent division.
3. The Identity Element: Preserving the Multiplication
In mathematics, an identity element is a number that, when used in an operation, leaves the other number unchanged. For multiplication, the identity element is 1. Let's consider this:
3<sup>m</sup> * 3<sup>n</sup> = 3<sup>(m+n)</sup>
If we let n = 0, we get:
3<sup>m</sup> * 3<sup>0</sup> = 3<sup>(m+0)</sup> = 3<sup>m</sup>
For this equation to hold true, 3<sup>0</sup> must equal 1, as multiplying by 1 leaves 3<sup>m</sup> unchanged. This reinforces the concept that 3<sup>0</sup> acts as the multiplicative identity.
Beyond 3<sup>0</sup>: Extending the Principle
The principle that any non-zero number raised to the power of zero equals 1 applies universally. This means:
- 10<sup>0</sup> = 1
- 100<sup>0</sup> = 1
- x<sup>0</sup> = 1 (where x is any non-zero number)
This consistent rule is fundamental to various mathematical operations and concepts.
Common Misconceptions and Addressing Them
Several misconceptions surround the concept of 0<sup>0</sup>. It's crucial to understand that 0<sup>0</sup> is undefined. This is because applying the pattern approach or the exponent division rule to 0 results in inconsistencies and contradictions. Therefore, it's essential to distinguish between 0 raised to the power of zero and other numbers raised to the power of zero.
Another frequent confusion arises from interpreting 3<sup>0</sup> as "no 3's," leading to the incorrect conclusion that it's 0. However, the exponent doesn't dictate the number of times the base is used in addition; it defines the number of times the base is used in multiplication.
Practical Applications: Real-World Relevance of Exponents
The concept of raising a number to the power of zero, seemingly abstract, finds numerous applications in various fields:
1. Computer Science: Counting and Combinatorics
In computer science, exponents play a crucial role in counting operations, particularly in combinatorics and algorithm analysis. Understanding zero exponents aids in simplifying calculations and determining the efficiency of various algorithms.
2. Physics and Engineering: Exponential Decay and Growth
Exponential functions, which heavily rely on exponents, model phenomena involving exponential growth or decay. These models are used to describe radioactive decay, population growth, and many other processes in physics and engineering.
3. Finance: Compound Interest
The concept of compound interest relies heavily on exponential functions. Understanding exponents is essential for calculating interest earned over time. The principle of 3<sup>0</sup> =1 is implicitly used in calculations that deal with the compounding principle over time.
4. Mathematics: Simplifying Expressions
Understanding 3<sup>0</sup> = 1 simplifies various algebraic manipulations and equation solving. It streamlines calculations and provides a crucial tool for simplifying complex expressions.
Conclusion: Mastering Exponents for a Deeper Understanding
The seemingly simple question, "What is 3 to the zeroth power?" leads to a deeper appreciation of the elegance and consistency inherent in mathematical principles. The fact that 3<sup>0</sup> = 1, while perhaps initially counterintuitive, stems from a logical extension of the rules governing exponents. Understanding this principle is fundamental for anyone delving into mathematics, computer science, or any field requiring quantitative analysis. By grasping the underlying logic and appreciating the consistent pattern, we can use this knowledge to tackle more complex mathematical problems. Mastering this concept unlocks doors to a more profound understanding of exponentials and their diverse applications across numerous fields.
Latest Posts
Latest Posts
-
What Do Alvin And The Chipmunks Want For Christmas
Apr 01, 2025
-
What Provides The Means Of Storing Transmitting
Apr 01, 2025
-
A Desk Is How Many Meters High
Apr 01, 2025
-
How Many Ounces Of Peanut Butter Are In A Cup
Apr 01, 2025
-
How Many Times Does 7 Go Into 9
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about What Is 3 To The Zeroth Power . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
