What Is 4 To The 0 Power
Arias News
Mar 28, 2025 · 5 min read
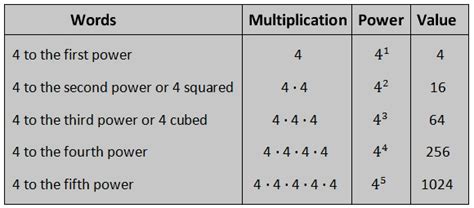
Table of Contents
What is 4 to the 0 Power? Unraveling the Mystery of Exponents
The seemingly simple question, "What is 4 to the 0 power?" can lead to surprising insights into the fundamental rules governing exponents and mathematics as a whole. While it might seem counterintuitive at first, understanding this concept unlocks a deeper appreciation of mathematical consistency and elegance. This article will delve into the meaning of 4<sup>0</sup>, explore the broader context of zero exponents, and demonstrate why the answer, 1, is not arbitrary but a logical consequence of mathematical principles.
Understanding Exponents: A Quick Refresher
Before tackling the enigma of 4<sup>0</sup>, let's solidify our understanding of exponents. An exponent, also known as a power or index, indicates how many times a base number is multiplied by itself. For example:
- 4<sup>1</sup> = 4 (4 multiplied by itself once)
- 4<sup>2</sup> = 16 (4 multiplied by itself twice: 4 x 4)
- 4<sup>3</sup> = 64 (4 multiplied by itself three times: 4 x 4 x 4)
- 4<sup>4</sup> = 256 (4 multiplied by itself four times: 4 x 4 x 4 x 4)
Notice a pattern? As the exponent increases by one, the result is multiplied by the base (4). This consistent pattern is crucial to understanding what happens when the exponent is zero.
The Curious Case of 4<sup>0</sup>: Why It Equals 1
The rule for any non-zero number raised to the power of zero is that it equals 1. Thus, 4<sup>0</sup> = 1. But why? Several approaches can illustrate this fundamental principle:
1. The Pattern Approach: Maintaining Consistency
Let's continue the pattern we observed earlier, but this time, let's move down in exponents:
- 4<sup>4</sup> = 256
- 4<sup>3</sup> = 64 (256 / 4)
- 4<sup>2</sup> = 16 (64 / 4)
- 4<sup>1</sup> = 4 (16 / 4)
Following this consistent pattern of division by the base, the next logical step is:
- 4<sup>0</sup> = 1 (4 / 4)
This demonstrates that defining 4<sup>0</sup> as 1 maintains the established pattern of dividing by the base as the exponent decreases. This consistency is a cornerstone of mathematical elegance and predictability.
2. The Rule of Exponents: a<sup>m</sup> / a<sup>n</sup> = a<sup>(m-n)</sup>
One of the fundamental rules of exponents states that when dividing two numbers with the same base, you subtract the exponents. Let's apply this rule:
Let's consider 4<sup>2</sup> / 4<sup>2</sup>. Using the rule of exponents:
4<sup>2</sup> / 4<sup>2</sup> = 4<sup>(2-2)</sup> = 4<sup>0</sup>
However, we also know that any number divided by itself equals 1. Therefore:
4<sup>2</sup> / 4<sup>2</sup> = 16 / 16 = 1
Thus, we conclude that 4<sup>0</sup> must equal 1 to maintain the consistency of the exponent rules.
3. The Identity Element: Multiplying by 1
In mathematics, the number 1 is the multiplicative identity. This means that multiplying any number by 1 leaves the number unchanged. Consider this expression:
4<sup>3</sup> x 4<sup>0</sup>
Using the rule of exponents for multiplication (add the exponents), we get:
4<sup>(3+0)</sup> = 4<sup>3</sup> = 64
For this equation to remain true, 4<sup>0</sup> must be equal to 1 because 64 x 1 = 64. This illustrates how defining 4<sup>0</sup> as 1 preserves the multiplicative identity.
Expanding the Concept Beyond 4: The Generality of a<sup>0</sup> = 1
The principle of a<sup>0</sup> = 1 applies to any non-zero number 'a'. Whether it's 10<sup>0</sup>, (-5)<sup>0</sup>, or (1/2)<sup>0</sup>, the result will always be 1. This universality underscores the importance of this rule within the broader mathematical framework.
Important Note: The expression 0<sup>0</sup> is undefined. This is a separate mathematical consideration and is not covered by the general rule a<sup>0</sup> = 1. The reason for this is rooted in conflicting definitions and potential inconsistencies that arise when considering limits and different mathematical contexts.
Practical Applications: Where Does This Matter?
The concept of zero exponents might seem purely theoretical, but it has significant implications across various fields:
-
Algebra: Understanding zero exponents is critical for simplifying algebraic expressions, solving equations, and manipulating variables effectively.
-
Calculus: The concept plays a crucial role in derivative and integral calculations, particularly when dealing with functions involving exponentials.
-
Computer Science: In programming and algorithm design, understanding exponential notation is essential for analyzing algorithm efficiency and complexity. Many data structures and algorithms rely on exponential functions, and understanding the base case of a zero exponent is foundational.
-
Physics and Engineering: Many physical phenomena are described by exponential functions, such as radioactive decay, population growth, and compound interest. Accurate modeling of these processes depends heavily on a correct understanding of exponential notation, including the case of a zero exponent.
-
Finance: Compound interest calculations, which are fundamental to many financial models, utilize exponential functions. The correct handling of exponents, including zero exponents, ensures accurate financial calculations.
Conclusion: The Elegance of Mathematical Consistency
The answer to "What is 4 to the 0 power?" is not a random assignment but a direct consequence of maintaining consistency within the rules of exponents. The principle that any non-zero number raised to the power of zero equals 1 is a fundamental concept in mathematics, and understanding it is essential for a deeper understanding of numerous mathematical and scientific disciplines. By exploring the patterns, applying the rules of exponents, and considering the multiplicative identity, we’ve clearly demonstrated why 4<sup>0</sup> = 1 and why this principle extends to all non-zero bases. This elegant consistency is a testament to the beauty and power of mathematical principles. From algebra to advanced calculus, understanding this seemingly simple concept provides a solid foundation for further mathematical exploration.
Latest Posts
Latest Posts
-
What Is One Percent Of 10 Billion
Mar 31, 2025
-
How Tall Is 35 Inches In Feet
Mar 31, 2025
-
How Much Is 6 Grams Of Sugar
Mar 31, 2025
-
What Did The Chef Say To The Hungry Watch
Mar 31, 2025
-
What Is A 15 Out Of 19
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about What Is 4 To The 0 Power . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
