What Is 4 To The 2 Power
Arias News
May 08, 2025 · 5 min read
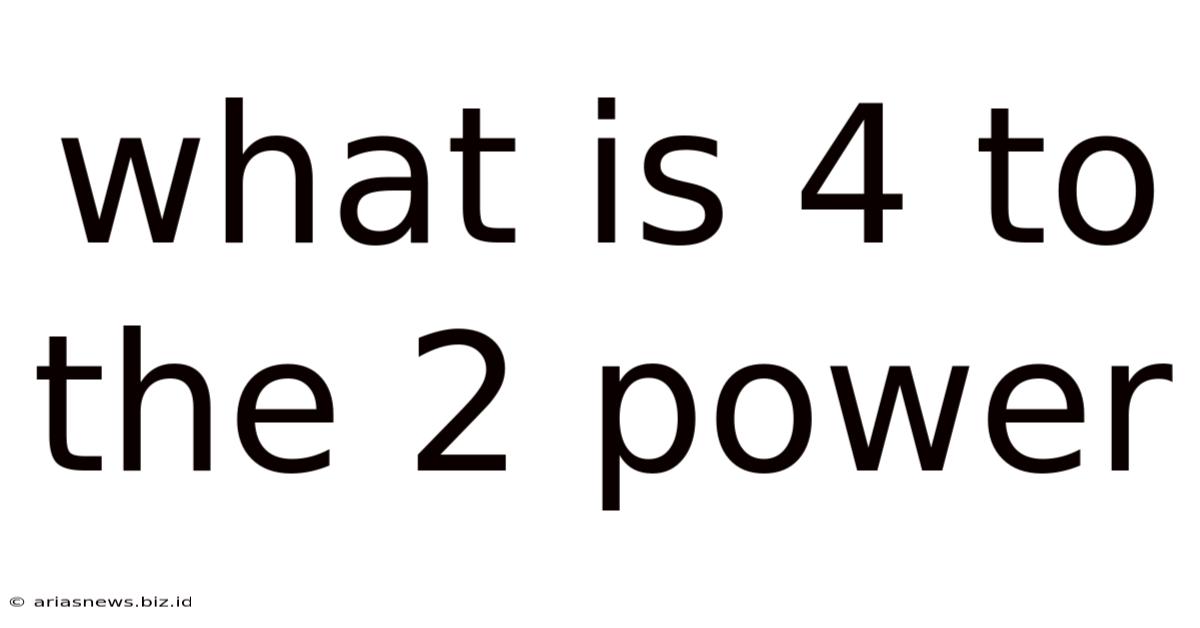
Table of Contents
What is 4 to the 2nd Power? A Deep Dive into Exponents and Their Applications
Understanding exponents is fundamental to mathematics and numerous fields. This comprehensive guide will explore the meaning of "4 to the 2nd power" (often written as 4² or 4<sup>2</sup>), delve into the broader concept of exponents, and illustrate their applications in various real-world scenarios. We'll cover everything from basic calculations to more advanced concepts, ensuring a thorough understanding for both beginners and those seeking a refresher.
Understanding Exponents: The Basics
Before tackling 4 to the 2nd power specifically, let's establish a solid foundation in exponents. An exponent, also known as a power or index, indicates how many times a number (the base) is multiplied by itself. The general form is:
b<sup>n</sup>
Where:
- b represents the base (the number being multiplied).
- n represents the exponent (the number of times the base is multiplied by itself).
For example, 2<sup>3</sup> (2 to the 3rd power) means 2 × 2 × 2 = 8. The base is 2, and the exponent is 3.
Calculating 4 to the 2nd Power (4²)
Now, let's address the question directly: What is 4 to the 2nd power? This is represented as 4². Following the definition of exponents, this means:
4² = 4 × 4 = 16
Therefore, 4 to the 2nd power is equal to 16. This is a relatively simple calculation, but it forms the basis for understanding more complex exponential expressions.
Expanding on Exponents: Properties and Rules
Exponents follow specific rules and properties that are crucial for performing calculations efficiently and accurately. Here are some key properties:
1. Product of Powers:
When multiplying two numbers with the same base, you add their exponents:
b<sup>m</sup> × b<sup>n</sup> = b<sup>(m+n)</sup>
For example: 2³ × 2² = 2<sup>(3+2)</sup> = 2⁵ = 32
2. Quotient of Powers:
When dividing two numbers with the same base, you subtract their exponents:
b<sup>m</sup> ÷ b<sup>n</sup> = b<sup>(m-n)</sup>
For example: 2⁵ ÷ 2² = 2<sup>(5-2)</sup> = 2³ = 8
3. Power of a Power:
When raising a power to another power, you multiply the exponents:
(b<sup>m</sup>)<sup>n</sup> = b<sup>(m×n)</sup>
For example: (2²)³ = 2<sup>(2×3)</sup> = 2⁶ = 64
4. Power of a Product:
When raising a product to a power, you raise each factor to that power:
(a × b)<sup>n</sup> = a<sup>n</sup> × b<sup>n</sup>
For example: (2 × 3)² = 2² × 3² = 4 × 9 = 36
5. Power of a Quotient:
When raising a quotient to a power, you raise both the numerator and the denominator to that power:
(a ÷ b)<sup>n</sup> = a<sup>n</sup> ÷ b<sup>n</sup>
For example: (2 ÷ 3)² = 2² ÷ 3² = 4 ÷ 9 = 4/9
Exponents with Zero and Negative Exponents
The rules extend to exponents of zero and negative numbers:
-
b⁰ = 1 (Any non-zero base raised to the power of zero equals 1)
-
b<sup>-n</sup> = 1/b<sup>n</sup> (A negative exponent indicates the reciprocal of the base raised to the positive exponent)
Applications of Exponents in Real Life
Exponents are far from being a purely theoretical concept; they have wide-ranging practical applications across numerous fields:
1. Finance: Compound Interest
Compound interest calculations heavily rely on exponents. The formula for compound interest is:
A = P (1 + r/n)<sup>nt</sup>
Where:
- A = the future value of the investment/loan, including interest
- P = the principal investment amount (the initial deposit or loan amount)
- r = the annual interest rate (decimal)
- n = the number of times that interest is compounded per year
- t = the number of years the money is invested or borrowed for
The exponent nt demonstrates how the interest compounds over time, significantly impacting the final amount.
2. Science: Exponential Growth and Decay
Many natural phenomena, such as population growth, radioactive decay, and the spread of diseases, exhibit exponential growth or decay. These processes are modeled using exponential functions, which incorporate exponents to describe the rate of change.
3. Computer Science: Binary Numbers and Data Storage
Computers operate using binary code (base-2), which represents data using only two digits: 0 and 1. Exponents are crucial in understanding how large numbers are represented and processed in binary systems, underpinning the functioning of computers and data storage.
4. Engineering: Calculating Volumes and Areas
Exponents are fundamental in geometric calculations. For example, the volume of a cube is calculated as side³, and the area of a square is side².
Beyond the Basics: More Complex Exponents
While 4² is a straightforward calculation, the concept of exponents extends to fractional and irrational exponents.
Fractional Exponents: Roots
Fractional exponents represent roots. For example:
- b<sup>1/n</sup> = <sup>n</sup>√b (The nth root of b)
This means that b<sup>1/2</sup> is the square root of b, b<sup>1/3</sup> is the cube root of b, and so on.
Irrational Exponents: e and Natural Logarithms
Irrational exponents, such as e (Euler's number, approximately 2.71828), are used in advanced mathematical concepts like exponential functions and natural logarithms. These have crucial applications in calculus, statistics, and various scientific models.
Conclusion: Mastering Exponents for a Broader Understanding
Understanding exponents, starting with simple examples like 4², is crucial for progress in mathematics and numerous related fields. From financial calculations to scientific modeling, the applications are vast and impactful. By grasping the fundamental properties and rules of exponents, along with their real-world applications, you equip yourself with a powerful tool for problem-solving and a deeper understanding of the mathematical world around us. This article has provided a solid foundation; further exploration of more advanced topics like logarithms and calculus will enhance your understanding even further. Remember to practice regularly to solidify your comprehension and build confidence in tackling complex exponential problems.
Latest Posts
Latest Posts
-
How Many Square Feet Are In A Yard Of Concrete
May 08, 2025
-
How Many Tons Are In 3000 Pounds
May 08, 2025
-
How Fast Is 113 Km In Mph
May 08, 2025
-
Why Does Marty Stuart Wear Scarves Around His Neck
May 08, 2025
-
What Is The Square Footage Of A Quarter Acre
May 08, 2025
Related Post
Thank you for visiting our website which covers about What Is 4 To The 2 Power . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.