What Is 4 To The 5th Power
Arias News
Mar 30, 2025 · 5 min read
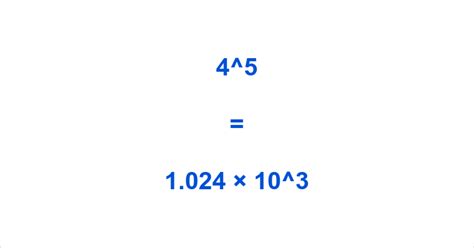
Table of Contents
What is 4 to the 5th Power? A Deep Dive into Exponentiation
Understanding exponents is fundamental to mathematics, forming the bedrock for many advanced concepts. This article delves into the seemingly simple question: "What is 4 to the 5th power?" We'll not only answer this directly but also explore the broader context of exponentiation, its properties, applications, and practical uses. We'll cover everything from the basics to more advanced considerations, ensuring a comprehensive understanding for readers of all levels.
Understanding Exponents: The Basics
Before tackling 4 to the 5th power, let's establish a solid foundation in exponential notation. An exponent, also known as a power or index, indicates how many times a base number is multiplied by itself. The general form is:
b<sup>n</sup>
Where:
- b is the base number (the number being multiplied).
- n is the exponent (the number of times the base is multiplied).
For example, 2<sup>3</sup> (2 to the power of 3) means 2 multiplied by itself three times: 2 * 2 * 2 = 8. This is also commonly read as "2 cubed."
Calculating 4 to the 5th Power
Now, let's address the main question: What is 4 to the 5th power (4<sup>5</sup>)? This translates to multiplying 4 by itself five times:
4<sup>5</sup> = 4 * 4 * 4 * 4 * 4 = 1024
Therefore, 4 to the 5th power is 1024.
Properties of Exponents: Rules and Relationships
Understanding the properties of exponents is crucial for simplifying complex expressions and solving equations. Here are some key properties:
1. Product of Powers:
When multiplying two numbers with the same base, you add the exponents:
b<sup>m</sup> * b<sup>n</sup> = b<sup>(m+n)</sup>
For example: 2<sup>3</sup> * 2<sup>2</sup> = 2<sup>(3+2)</sup> = 2<sup>5</sup> = 32
2. Quotient of Powers:
When dividing two numbers with the same base, you subtract the exponents:
b<sup>m</sup> / b<sup>n</sup> = b<sup>(m-n)</sup>
For example: 2<sup>5</sup> / 2<sup>2</sup> = 2<sup>(5-2)</sup> = 2<sup>3</sup> = 8
3. Power of a Power:
When raising a power to another power, you multiply the exponents:
(b<sup>m</sup>)<sup>n</sup> = b<sup>(m*n)</sup>
For example: (2<sup>3</sup>)<sup>2</sup> = 2<sup>(3*2)</sup> = 2<sup>6</sup> = 64
4. Power of a Product:
When raising a product to a power, you raise each factor to that power:
(ab)<sup>n</sup> = a<sup>n</sup>b<sup>n</sup>
For example: (2 * 3)<sup>2</sup> = 2<sup>2</sup> * 3<sup>2</sup> = 4 * 9 = 36
5. Power of a Quotient:
When raising a quotient to a power, you raise both the numerator and the denominator to that power:
(a/b)<sup>n</sup> = a<sup>n</sup>/b<sup>n</sup>
For example: (2/3)<sup>2</sup> = 2<sup>2</sup>/3<sup>2</sup> = 4/9
Understanding and applying these properties simplifies complex calculations involving exponents significantly.
Applications of Exponentiation: Real-World Examples
Exponentiation isn't just a theoretical concept; it has numerous real-world applications across various fields:
1. Compound Interest:
Calculating compound interest relies heavily on exponentiation. The formula involves raising the principal amount plus the interest rate to the power of the number of compounding periods.
2. Population Growth:
Predicting population growth often uses exponential models. The exponential function accurately reflects the rapid increase in population size over time.
3. Radioactive Decay:
The decay of radioactive materials follows an exponential decay pattern. Exponentiation plays a vital role in determining the remaining amount of radioactive substance after a certain period.
4. Computer Science:
Exponentiation is crucial in computer science, especially in algorithms and data structures. Big O notation, used to analyze algorithm efficiency, frequently employs exponential functions to represent the growth of computational complexity.
5. Finance and Economics:
Many financial models use exponential functions to analyze growth and decay. For example, the present value of future cash flows often involves exponential discounting.
Beyond the Basics: Negative and Fractional Exponents
Our exploration has so far focused on positive integer exponents. However, exponents can also be negative or fractional, extending the scope of exponentiation further.
1. Negative Exponents:
A negative exponent means the reciprocal of the base raised to the positive exponent:
b<sup>-n</sup> = 1/b<sup>n</sup>
For example: 2<sup>-3</sup> = 1/2<sup>3</sup> = 1/8
2. Fractional Exponents:
Fractional exponents involve roots and powers. The numerator represents the power, and the denominator represents the root:
b<sup>m/n</sup> = (<sup>n</sup>√b)<sup>m</sup> = <sup>n</sup>√(b<sup>m</sup>)
For example: 8<sup>2/3</sup> = (<sup>3</sup>√8)<sup>2</sup> = 2<sup>2</sup> = 4
Advanced Topics in Exponentiation
For those interested in further exploration, here are some advanced topics related to exponentiation:
-
Logarithms: Logarithms are the inverse of exponentiation. They provide a way to solve for the exponent when the base and the result are known.
-
Exponential Functions: These functions have the form f(x) = b<sup>x</sup>, where 'b' is the base. They are used extensively in modeling various phenomena, including growth, decay, and oscillations.
-
Complex Numbers: Exponentiation can be extended to complex numbers, resulting in complex-valued functions with interesting geometric interpretations.
Conclusion: Mastering Exponentiation
This detailed exploration of "What is 4 to the 5th power?" has transcended a simple numerical calculation, providing a comprehensive understanding of exponentiation, its properties, applications, and advanced extensions. From the fundamental concept of repeated multiplication to the intricacies of negative and fractional exponents, we've covered the ground thoroughly. By mastering the principles outlined here, you'll not only be able to solve exponential problems but also appreciate their widespread significance in diverse fields, solidifying your mathematical foundation. Remember to practice regularly, applying these concepts to various problems to solidify your understanding and enhance your problem-solving skills. The ability to confidently work with exponents is a valuable asset in various academic and professional settings.
Latest Posts
Latest Posts
-
How Many Minutes Drive Is 5 Miles
Apr 01, 2025
-
What Percentage Is 11 Out Of 15
Apr 01, 2025
-
What Year Were You Born If Your 31
Apr 01, 2025
-
How Many Cups Are In 3 Lbs Of Sour Cream
Apr 01, 2025
-
Do They Check For Warrants At The Emergency Room
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about What Is 4 To The 5th Power . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
