What Is 4 To The Power Of 1
Arias News
May 10, 2025 · 6 min read
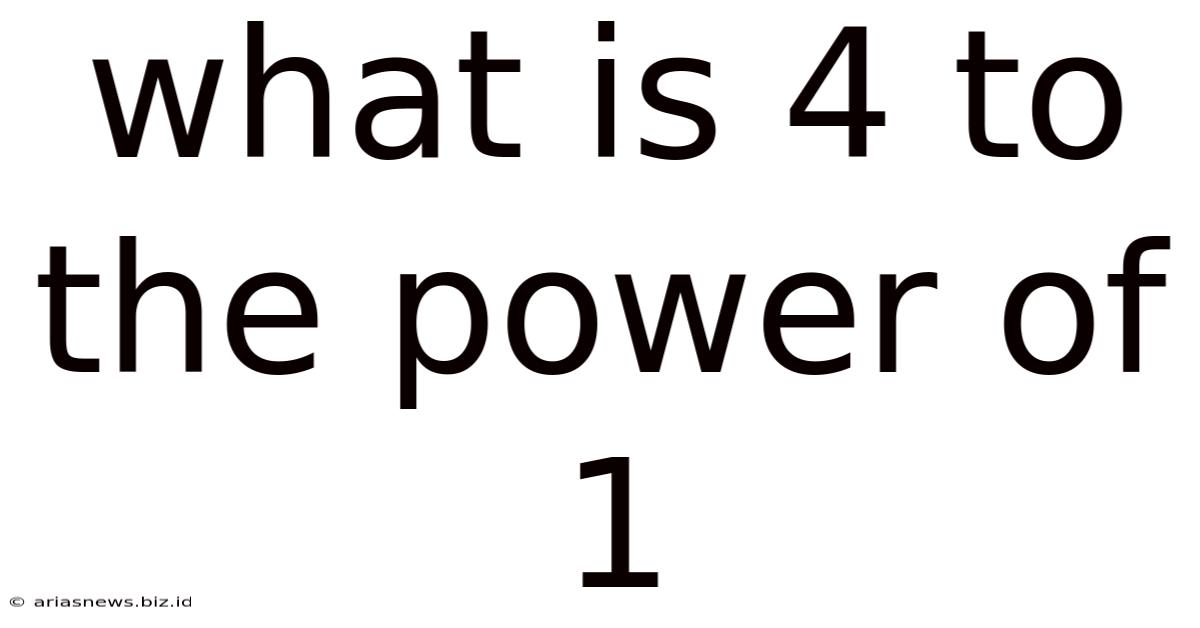
Table of Contents
What is 4 to the Power of 1? A Deep Dive into Exponents and Their Applications
The seemingly simple question, "What is 4 to the power of 1?", opens a door to a vast and fascinating world of mathematics: exponents. While the answer itself is straightforward – 4 – understanding the underlying principles unlocks a deeper appreciation of exponential growth, its applications in various fields, and the broader context of mathematical operations. This article will explore this fundamental concept, expanding on its implications and real-world relevance.
Understanding Exponents: The Basics
Before we delve into the specifics of 4<sup>1</sup>, let's establish a solid understanding of exponents. An exponent, also known as a power or index, indicates how many times a number (the base) is multiplied by itself. It's written as a superscript to the right of the base.
For example, in the expression 5<sup>3</sup> (5 to the power of 3 or 5 cubed):
- 5 is the base.
- 3 is the exponent.
This expression signifies 5 multiplied by itself three times: 5 x 5 x 5 = 125.
The Significance of Exponent 1
Now, let's address our core question: 4<sup>1</sup>. This expression represents the base 4 raised to the power of 1. According to the definition of exponents, this means multiplying 4 by itself one time. Therefore:
4<sup>1</sup> = 4
This might seem trivial, but it highlights a crucial property of exponents: any number raised to the power of 1 is equal to itself. This is a fundamental rule that underpins more complex exponential operations.
Exploring Different Bases and Exponents: A Comparative Analysis
To further solidify our understanding, let's compare 4<sup>1</sup> with other examples, varying both the base and the exponent:
Varying the Base:
- 1<sup>1</sup> = 1: One raised to the power of one equals one.
- 10<sup>1</sup> = 10: Ten raised to the power of one equals ten.
- 100<sup>1</sup> = 100: One hundred raised to the power of one equals one hundred.
This demonstrates the consistent rule: any number raised to the power of 1 equals that number.
Varying the Exponent:
Let's keep the base as 4 and change the exponent:
- 4<sup>0</sup> = 1: Any non-zero number raised to the power of zero equals one. This is a separate rule in exponent mathematics.
- 4<sup>2</sup> = 16: Four squared (4 to the power of 2) equals 16 (4 x 4).
- 4<sup>3</sup> = 64: Four cubed (4 to the power of 3) equals 64 (4 x 4 x 4).
- 4<sup>4</sup> = 256: Four to the power of 4 equals 256 (4 x 4 x 4 x 4).
This illustrates how the value changes significantly as the exponent increases. The difference between 4<sup>1</sup> and 4<sup>4</sup>, for instance, showcases the exponential growth that characterizes higher powers.
Real-World Applications of Exponents
The concept of exponents, even at its most basic level (like 4<sup>1</sup>), has extensive real-world applications across various disciplines:
1. Compound Interest: The Power of Exponential Growth
One of the most practical applications of exponents is in calculating compound interest. Compound interest is interest earned not only on the principal amount but also on accumulated interest. The formula for compound interest involves exponents:
A = P (1 + r/n)<sup>nt</sup>
Where:
- A = the future value of the investment/loan, including interest
- P = the principal investment amount (the initial deposit or loan amount)
- r = the annual interest rate (decimal)
- n = the number of times that interest is compounded per year
- t = the number of years the money is invested or borrowed for
The exponent 'nt' highlights the exponential growth of the investment over time. Even a small increase in the interest rate or the investment period leads to a significantly larger return due to the exponential nature of the calculation. Understanding exponents is crucial for making informed financial decisions.
2. Population Growth: Modeling Exponential Increase
Exponents are also vital in modeling population growth. In scenarios with consistent birth and death rates, population growth can be approximated using exponential functions. The formula often involves a base representing the growth rate and an exponent representing the time period.
3. Radioactive Decay: Modeling Exponential Decrease
Conversely, exponential functions are used to model radioactive decay. The amount of radioactive material decreases exponentially over time. The exponent in the decay formula represents the time elapsed.
4. Computer Science: Binary Numbers and Data Storage
In computer science, exponents are fundamental to understanding binary numbers, the foundation of digital information. Binary numbers use only two digits (0 and 1), and the place value of each digit is a power of 2. For instance, the binary number 1011 is equal to 1 x 2<sup>3</sup> + 0 x 2<sup>2</sup> + 1 x 2<sup>1</sup> + 1 x 2<sup>0</sup> = 8 + 0 + 2 + 1 = 11 in decimal.
5. Scientific Notation: Expressing Very Large or Very Small Numbers
Scientific notation utilizes exponents to express extremely large or small numbers concisely. It's commonly used in science and engineering to represent quantities like the distance between stars or the size of atoms. For example, the speed of light is approximately 3 x 10<sup>8</sup> meters per second.
Beyond the Basics: Exploring More Complex Exponential Concepts
Understanding 4<sup>1</sup> opens the door to more advanced concepts in mathematics:
1. Negative Exponents: Reciprocals
Negative exponents indicate reciprocals. For instance, 4<sup>-1</sup> is equal to 1/4<sup>1</sup> = 1/4. This extends the concept of exponents to encompass fractional values.
2. Fractional Exponents: Roots
Fractional exponents represent roots. For example, 4<sup>1/2</sup> is the square root of 4, which is 2. 4<sup>1/3</sup> is the cube root of 4. This introduces the concept of radicals and their relationship to exponents.
3. Exponential Functions and Graphs
Exponential functions, where the variable is in the exponent, exhibit characteristic curves that represent exponential growth or decay. Understanding these graphs is crucial in various fields, from finance to biology.
4. Logarithms: The Inverse of Exponents
Logarithms are the inverse of exponential functions. They allow us to find the exponent given the base and the result. Logarithms are widely used in scientific calculations and problem-solving.
5. Complex Numbers and Exponential Functions
In advanced mathematics, exponents are extended to encompass complex numbers, leading to fascinating relationships between exponential functions and trigonometric functions, described by Euler's formula (e<sup>ix</sup> = cos(x) + i sin(x)).
Conclusion: The Enduring Importance of a Simple Concept
While the answer to "What is 4 to the power of 1?" is simply 4, the implications of this seemingly basic mathematical concept are far-reaching. Understanding exponents is crucial for grasping exponential growth and decay, essential for comprehending numerous phenomena in various scientific, financial, and technological domains. From compound interest to population dynamics, from computer science to scientific notation, exponents are a cornerstone of mathematical understanding and their practical applications are limitless. The foundation laid by a simple understanding of exponents, such as 4<sup>1</sup>, serves as a crucial stepping stone to more advanced mathematical concepts and their real-world applications.
Latest Posts
Latest Posts
-
Does Mayo Go Bad After Expiration Date
May 10, 2025
-
How Much Shredded Cheese In 8 Oz Block
May 10, 2025
-
How Long Does It Take To Drive 33 Miles
May 10, 2025
-
Can I Use Permanent Hair Color Without Developer
May 10, 2025
-
How Old Am I If I Was Born 1999
May 10, 2025
Related Post
Thank you for visiting our website which covers about What Is 4 To The Power Of 1 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.