What Is 4 To The Power Of 5
Arias News
May 09, 2025 · 6 min read
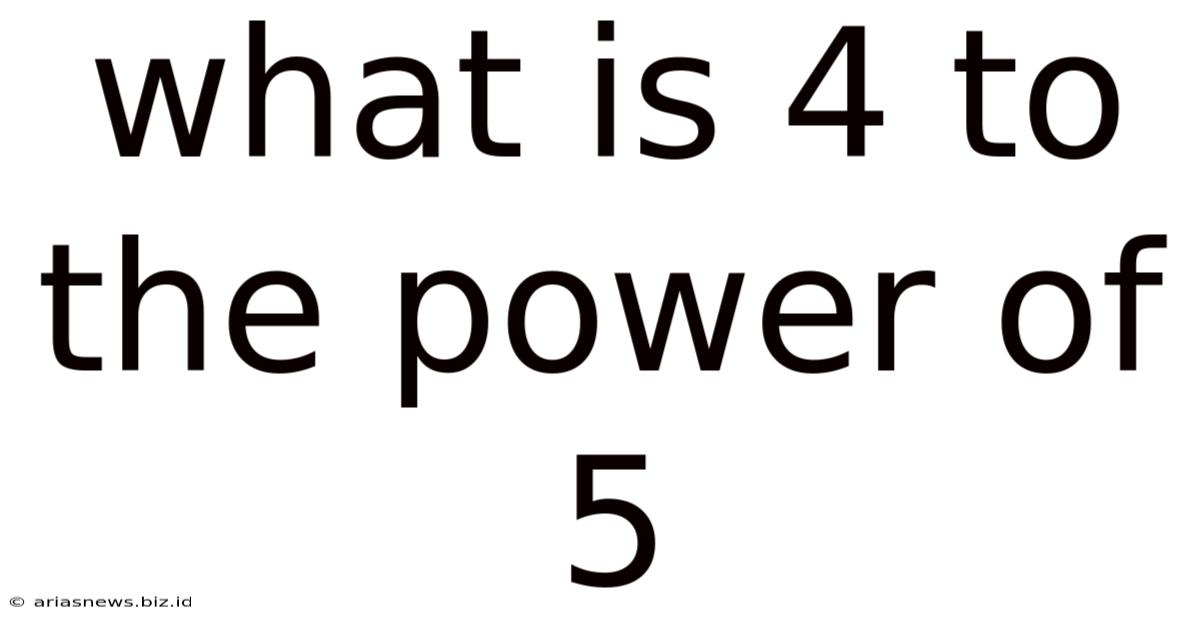
Table of Contents
What is 4 to the Power of 5? A Deep Dive into Exponentiation
The seemingly simple question, "What is 4 to the power of 5?" opens a door to a fascinating world of mathematics, specifically exponentiation. While the answer itself is straightforward – 1024 – understanding the underlying concepts and applications provides a much richer understanding. This article will delve into the meaning of exponents, explore different ways to calculate 4<sup>5</sup>, discuss its applications in various fields, and touch upon the broader implications of exponential growth.
Understanding Exponentiation: The Basics
Exponentiation, often expressed as "raising to a power" or "to the power of," is a mathematical operation involving two numbers: the base and the exponent. The base is the number being multiplied, and the exponent indicates how many times the base is multiplied by itself. In the expression 4<sup>5</sup>, 4 is the base and 5 is the exponent. This means we multiply 4 by itself five times: 4 x 4 x 4 x 4 x 4.
The Language of Exponents
It's crucial to understand the terminology. The expression 4<sup>5</sup> is read as "4 raised to the power of 5" or "4 to the fifth power." The superscript number (5) indicates the exponent. Other examples include:
- 2<sup>3</sup> (2 cubed or 2 to the power of 3): 2 x 2 x 2 = 8
- 5<sup>2</sup> (5 squared or 5 to the power of 2): 5 x 5 = 25
- 10<sup>4</sup> (10 to the power of 4): 10 x 10 x 10 x 10 = 10,000
Calculating 4 to the Power of 5: Methods and Approaches
There are several ways to calculate 4<sup>5</sup>, each offering a different perspective on this mathematical operation.
Method 1: Repeated Multiplication
This is the most straightforward approach, directly applying the definition of exponentiation:
4<sup>5</sup> = 4 x 4 x 4 x 4 x 4 = 1024
This method is easy to understand and execute, especially for smaller exponents. However, for larger exponents, it can become quite tedious.
Method 2: Using Properties of Exponents
Exponents possess several useful properties that simplify calculations. One particularly helpful property is the rule of multiplying powers with the same base: a<sup>m</sup> x a<sup>n</sup> = a<sup>(m+n)</sup>. We can break down 4<sup>5</sup> using this:
4<sup>5</sup> = 4<sup>2</sup> x 4<sup>2</sup> x 4<sup>1</sup> = 16 x 16 x 4 = 256 x 4 = 1024
This method might seem more complex initially, but it highlights the underlying structure of exponentiation and can be more efficient for larger numbers or when dealing with more complex exponential expressions.
Method 3: Using a Calculator or Computer
For larger exponents or when precision is paramount, using a calculator or a computer program is highly recommended. Most calculators have an exponent function (usually denoted by a ^ symbol or a x<sup>y</sup> button). Simply input 4, the exponent symbol, 5, and press equals (=) to get the answer: 1024.
Applications of 4 to the Power of 5 and Exponential Growth
The result of 4<sup>5</sup>, 1024, might seem like a simple number, but its significance extends far beyond a single mathematical calculation. Exponential growth, where a quantity increases by a fixed percentage over time, is ubiquitous in various fields. Understanding exponential growth is crucial for comprehending phenomena ranging from compound interest to population dynamics.
Compound Interest
In finance, compound interest is a powerful example of exponential growth. If you invest a principal amount with a fixed interest rate that compounds annually, your investment grows exponentially. The formula for compound interest is:
A = P (1 + r/n)<sup>nt</sup>
Where:
- A = the future value of the investment/loan, including interest
- P = the principal investment amount (the initial deposit or loan amount)
- r = the annual interest rate (decimal)
- n = the number of times that interest is compounded per year
- t = the number of years the money is invested or borrowed for
While 4<sup>5</sup> itself might not directly represent a compound interest calculation, the principle of exponential growth is directly applicable. The faster the compounding, the faster the exponential growth.
Population Growth (Under Ideal Conditions)
Under ideal conditions (unlimited resources, no predation, etc.), populations can grow exponentially. If a population doubles every year, the growth follows an exponential pattern. While real-world population growth is far more complex, understanding exponential models provides a valuable baseline for analysis and prediction. The exponent represents the number of doubling periods.
Computer Science: Data Structures and Algorithms
In computer science, exponential functions often appear in the analysis of algorithms and data structures. The time complexity of certain algorithms can be described using exponential functions. For example, the brute-force approach to solving certain problems might exhibit exponential time complexity, meaning that the computation time increases exponentially with the input size. Understanding this is crucial for optimizing algorithms and choosing efficient solutions.
Other Applications
Beyond these examples, exponential functions appear in various other fields, including:
- Physics: Radioactive decay, describing the exponential decrease in the amount of a radioactive substance over time.
- Biology: Modeling bacterial growth and the spread of diseases.
- Chemistry: Chemical reaction rates often follow exponential patterns.
- Engineering: Analyzing the strength of materials and designing structures.
Beyond 4 to the Power of 5: Exploring Larger Exponents and Exponential Functions
The concept of 4<sup>5</sup> provides a stepping stone to understanding larger exponents and the broader world of exponential functions. These functions are represented by equations of the form y = a<sup>x</sup>, where 'a' is the base and 'x' is the exponent. These functions are crucial for modeling various phenomena exhibiting exponential growth or decay.
Exponential Functions and Their Graphs
Graphing exponential functions reveals their characteristic shape: a steep curve that increases rapidly as x increases. This visualization powerfully illustrates the nature of exponential growth.
Logarithms: The Inverse of Exponentiation
Logarithms are the inverse operation of exponentiation. If we have y = a<sup>x</sup>, then the logarithm (base a) of y is x: log<sub>a</sub>(y) = x. Logarithms are invaluable for solving exponential equations and analyzing data that exhibit exponential behavior.
Exploring Larger Exponents: Computational Challenges
Calculating 4<sup>100</sup> or even larger exponents presents computational challenges. While calculators and computers can handle these, understanding the principles behind the calculations remains crucial. The sheer magnitude of such numbers emphasizes the power and potential of exponential growth.
Conclusion: The Significance of a Simple Calculation
The seemingly simple question of "What is 4 to the power of 5?" leads us to a deeper appreciation of exponentiation, its various applications, and the pervasive nature of exponential growth in the world around us. From understanding compound interest to modeling complex biological processes, the concepts explored here are vital for navigating a world increasingly shaped by exponential trends. The answer, 1024, is not just a number; it's a gateway to a profound understanding of mathematical principles and their real-world applications. Understanding these principles empowers us to make better informed decisions in finance, science, technology, and many other aspects of life.
Latest Posts
Latest Posts
-
In All Cases Of Erroneous Payment Resulting From Their Certification
May 09, 2025
-
How Much Is 38 Kg In Pounds
May 09, 2025
-
How Old Am I Born In 1955
May 09, 2025
-
How Much Is 97 Kg In Pounds
May 09, 2025
-
How Many Cups Is One Head Of Broccoli
May 09, 2025
Related Post
Thank you for visiting our website which covers about What Is 4 To The Power Of 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.