What Is 5 To The 5th Power
Arias News
Apr 01, 2025 · 4 min read
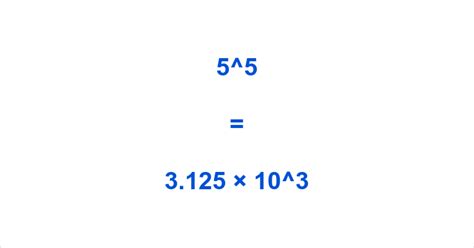
Table of Contents
What is 5 to the 5th Power? A Deep Dive into Exponentiation
Understanding exponents is fundamental to mathematics, forming the bedrock for numerous advanced concepts. This article delves into the seemingly simple question: "What is 5 to the 5th power?" We'll go beyond just providing the answer, exploring the underlying principles of exponentiation, its applications in various fields, and even touch upon some related mathematical curiosities.
Understanding Exponents: The Basics
Before we tackle 5 to the 5th power, let's solidify our understanding of exponential notation. An exponent, also known as a power or index, indicates how many times a base number is multiplied by itself. It's written as bⁿ, where 'b' represents the base and 'n' represents the exponent. This means 'b' is multiplied by itself 'n' times.
For example:
- 2³ (2 to the power of 3) means 2 × 2 × 2 = 8
- 10² (10 squared or 10 to the power of 2) means 10 × 10 = 100
- 4¹ (4 to the power of 1) simply means 4
Calculating 5 to the 5th Power
Now, let's address the main question: What is 5 to the 5th power (5⁵)? This translates to:
5 × 5 × 5 × 5 × 5
Performing the calculation step-by-step:
- 5 × 5 = 25
- 25 × 5 = 125
- 125 × 5 = 625
- 625 × 5 = 3125
Therefore, 5⁵ = 3125.
Beyond the Calculation: Applications of Exponentiation
The concept of exponentiation isn't just a mathematical exercise; it has profound real-world applications across numerous disciplines:
1. Compound Interest: The Power of Growth
One of the most practical applications is in finance, specifically calculating compound interest. Compound interest means earning interest on your initial investment and on the accumulated interest. The formula involves exponentiation:
A = P (1 + r/n)^(nt)
Where:
- A = the future value of the investment/loan, including interest
- P = the principal investment amount (the initial deposit or loan amount)
- r = the annual interest rate (decimal)
- n = the number of times that interest is compounded per year
- t = the number of years the money is invested or borrowed for
The exponential component, (1 + r/n)^(nt), shows how dramatically compound interest can increase your investment over time. Understanding this is crucial for long-term financial planning.
2. Scientific Notation: Handling Huge Numbers
In science, we often deal with incredibly large or incredibly small numbers. Exponentiation, through scientific notation, makes these numbers manageable. For example, the speed of light is approximately 3 x 10⁸ meters per second. This is far easier to work with than writing out 300,000,000.
3. Population Growth and Decay: Modeling Change Over Time
Exponential functions are frequently used to model population growth (or decay, in the case of radioactive substances). The rate of growth or decay is often proportional to the current population size, resulting in exponential increase or decrease over time. This is crucial in ecological studies and epidemiology.
4. Computer Science: Binary Numbers and Data Storage
In computer science, the binary system (base-2) relies heavily on exponents of 2. Each bit in a computer's memory can represent either 0 or 1, and larger units of data (bytes, kilobytes, megabytes, etc.) are powers of 2. Understanding this is fundamental to grasping how computers store and process information.
5. Physics: Exponential Decay and Half-Life
In physics, radioactive decay follows an exponential pattern. The half-life of a radioactive substance is the time it takes for half of the substance to decay. This decay is described using exponential functions.
Exploring Related Mathematical Concepts
Understanding 5 to the 5th power opens the door to exploring further mathematical concepts:
1. Negative Exponents: Reciprocals
What happens when the exponent is negative? A negative exponent signifies the reciprocal of the base raised to the positive exponent. For example:
5⁻² = 1/(5²) = 1/25
2. Fractional Exponents: Roots
Fractional exponents represent roots. For example:
5^(1/2) = √5 (the square root of 5) 5^(1/3) = ³√5 (the cube root of 5)
3. Zero Exponent: A Special Case
Any number (except 0) raised to the power of 0 equals 1. This is a fundamental rule in exponent mathematics. For instance:
5⁰ = 1
4. Large Exponents and Computational Challenges:
While calculating 5⁵ is straightforward, calculating extremely large exponents can pose computational challenges. Specialized algorithms and software are employed to handle such calculations efficiently.
5 to the 5th Power in Different Bases
While we've primarily focused on base 10 (our decimal system), we can express 5⁵ in other bases. For example, in binary (base 2), 3125 would have a significantly longer representation. Converting between bases is another area of mathematical exploration.
Conclusion: The Significance of Understanding Exponentiation
The seemingly simple question of "What is 5 to the 5th power?" serves as a gateway to a deeper understanding of exponentiation, a powerful mathematical tool with widespread applications. From financial modeling to scientific calculations and computer science, the principles of exponents are essential for comprehending and interacting with the world around us. This exploration has not only provided the answer (3125) but also illuminated the broader context and significance of this fundamental mathematical operation. Further exploration into logarithms, another closely related concept, would deepen this understanding even further. The journey of mathematical discovery is ongoing, and this seemingly simple calculation acts as a compelling starting point.
Latest Posts
Latest Posts
-
How Many Ounces Is 1 3 Cup Of Butter
Apr 02, 2025
-
Match The Exercise With The Muscle Group It Exercises
Apr 02, 2025
-
What Is A 16 Out Of 22
Apr 02, 2025
-
How Do You Say New Jersey In Spanish
Apr 02, 2025
-
How Many Cups Are In 14 Oz
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about What Is 5 To The 5th Power . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
