What Is 7 To The Power Of 3
Arias News
May 09, 2025 · 5 min read
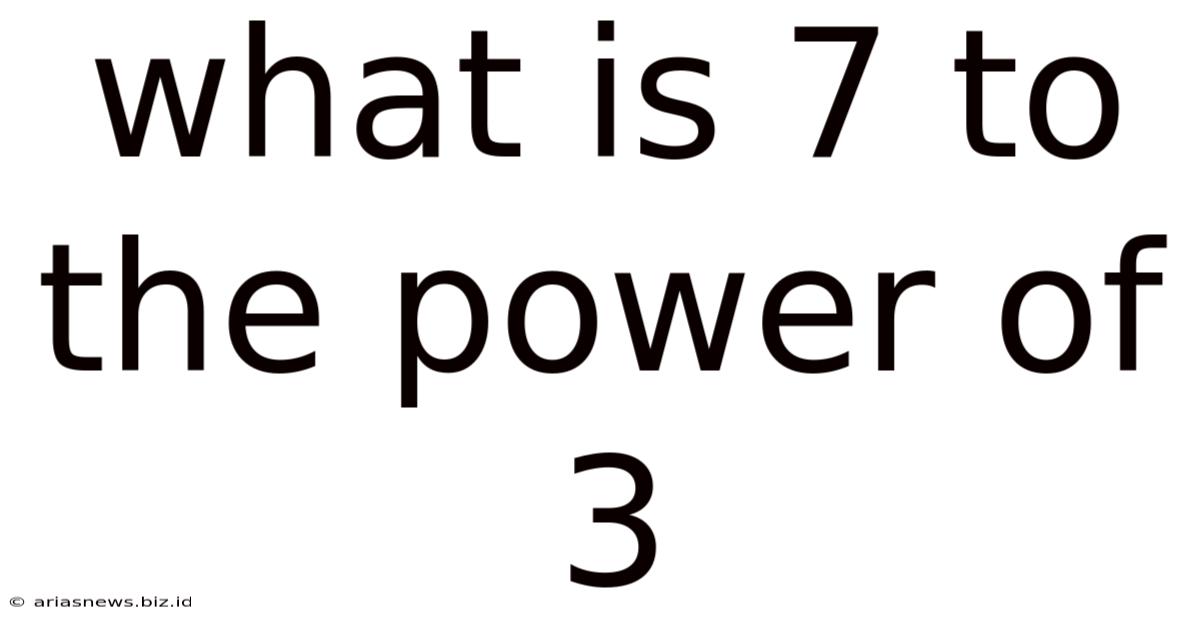
Table of Contents
What is 7 to the Power of 3? A Deep Dive into Exponentiation
The seemingly simple question, "What is 7 to the power of 3?" opens a door to a fascinating world of mathematics, specifically exponentiation. While the answer itself is straightforward – 343 – understanding the underlying concepts reveals the power and versatility of this fundamental mathematical operation. This article will not only answer the question directly but will also explore the broader context of exponents, their applications, and related mathematical principles.
Understanding Exponents: A Foundation in Mathematics
Exponentiation, at its core, is a shorthand way of representing repeated multiplication. The expression 7<sup>3</sup> (7 to the power of 3, or 7 cubed) means 7 multiplied by itself three times: 7 × 7 × 7. The base number (7 in this case) is the number being multiplied, and the exponent (3) indicates how many times the base is multiplied by itself.
Key Terminology:
- Base: The number being multiplied repeatedly (7 in 7<sup>3</sup>).
- Exponent (or Power or Index): The number indicating how many times the base is multiplied by itself (3 in 7<sup>3</sup>).
- Result (or Value): The outcome of the exponentiation (343 in 7<sup>3</sup>).
Understanding these terms is crucial for tackling more complex exponential problems.
Calculating 7 to the Power of 3
The calculation itself is relatively simple:
7 × 7 = 49 49 × 7 = 343
Therefore, 7 to the power of 3 is 343.
Expanding the Concept: Exponents Beyond 3
While we've focused on 7<sup>3</sup>, it's important to understand that exponents can be any number – positive integers, negative integers, fractions, even irrational numbers like π (pi). Let's briefly explore these:
Positive Integer Exponents:
These are the most straightforward type of exponents, representing repeated multiplication as shown above. For example:
- 7<sup>1</sup> = 7 (7 multiplied by itself once)
- 7<sup>2</sup> = 49 (7 squared, or 7 multiplied by itself twice)
- 7<sup>4</sup> = 2401 (7 multiplied by itself four times) and so on.
Zero Exponent:
Any number raised to the power of zero equals 1. This might seem counterintuitive, but it's a consistent mathematical rule:
7<sup>0</sup> = 1
This is based on the pattern of decreasing exponents: 7<sup>3</sup>/7<sup>1</sup> = 7<sup>2</sup>; 7<sup>2</sup>/7<sup>1</sup> = 7<sup>1</sup>; following this pattern, 7<sup>1</sup>/7<sup>1</sup> = 7<sup>0</sup> = 1.
Negative Exponents:
Negative exponents represent reciprocals. The expression 7<sup>-3</sup> is equivalent to 1/7<sup>3</sup>:
7<sup>-3</sup> = 1/343
Fractional Exponents (Rational Exponents):
Fractional exponents involve roots. For instance, 7<sup>1/2</sup> is the square root of 7, and 7<sup>1/3</sup> is the cube root of 7. More generally, 7<sup>m/n</sup> is equivalent to the nth root of 7<sup>m</sup>.
These fractional exponents significantly broaden the scope of exponentiation, allowing us to work with non-integer values.
Irrational Exponents:
Exponents can also be irrational numbers, such as π (approximately 3.14159). Calculating 7<sup>π</sup> requires advanced mathematical techniques, often involving series approximations.
Applications of Exponentiation
Exponentiation isn't just a theoretical concept; it has wide-ranging applications across numerous fields:
Science and Engineering:
- Exponential Growth and Decay: Many natural phenomena, such as population growth, radioactive decay, and compound interest, follow exponential patterns. The exponent plays a crucial role in modeling these processes.
- Physics: Exponentiation appears in various physical laws and equations, including those related to gravity, electromagnetism, and quantum mechanics.
- Engineering: Exponential functions are used in designing structures, analyzing circuits, and modeling various engineering systems.
Computer Science:
- Algorithms: Many computer algorithms, particularly those related to searching and sorting, have time complexities expressed using exponential notation (e.g., O(2<sup>n</sup>)). This indicates how the runtime of the algorithm scales with the input size.
- Data Structures: Exponential concepts are important in understanding data structures like trees and graphs.
- Cryptography: Cryptography relies heavily on exponentiation for encryption and decryption algorithms. The difficulty of calculating discrete logarithms underlies the security of many cryptographic systems.
Finance:
- Compound Interest: The calculation of compound interest uses exponential functions to determine the future value of an investment.
- Financial Modeling: Exponentials are integral to various financial models used for pricing options, valuing assets, and forecasting market trends.
Biology:
- Population Growth: Modeling population growth of organisms frequently uses exponential equations.
- Bacterial Growth: Similar to population growth, the exponential function helps in predicting bacterial growth.
Beyond the Basics: Logarithms and Their Relation to Exponents
Logarithms are the inverse function of exponentiation. If 7<sup>3</sup> = 343, then the logarithm base 7 of 343 is 3 (log<sub>7</sub>343 = 3). Logarithms are particularly useful for solving equations involving exponents and simplifying calculations.
Conclusion: The Significance of 7<sup>3</sup> and Exponentiation
While the answer to "What is 7 to the power of 3?" is simply 343, the journey to reach that answer has revealed the rich and diverse world of exponentiation. From its foundational definition as repeated multiplication to its far-reaching applications across numerous scientific, technological, and financial domains, exponentiation is a powerful tool that underpins many aspects of our understanding of the universe and the systems we build. Understanding the concept of exponents, its variations, and its relationship to logarithms is fundamental to appreciating the elegant and powerful nature of mathematics. The seemingly simple calculation of 7<sup>3</sup> = 343 serves as a gateway to a much deeper and more extensive mathematical landscape.
Latest Posts
Latest Posts
-
How To Write 3 Million In Numbers
May 09, 2025
-
Square Feet In 24 Foot Round Pool
May 09, 2025
-
18k Ge A In A Circle Meaning
May 09, 2025
-
What Grade Are You In At 15
May 09, 2025
-
1 Kilo Of Rice Is How Many Cups
May 09, 2025
Related Post
Thank you for visiting our website which covers about What Is 7 To The Power Of 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.