What Is 9 To The Power Of 4
Arias News
May 09, 2025 · 5 min read
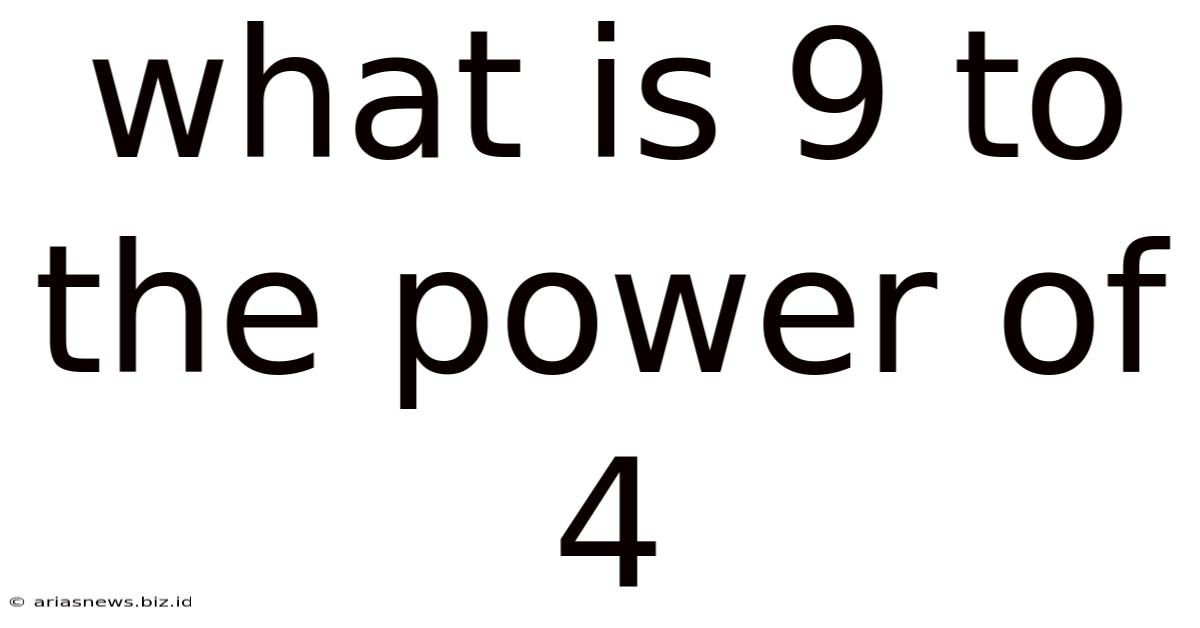
Table of Contents
What is 9 to the Power of 4? A Deep Dive into Exponentiation
The seemingly simple question, "What is 9 to the power of 4?" opens a door to a fascinating world of mathematics, specifically exponentiation. While the answer itself is straightforward – 6561 – the journey to understanding how we arrive at that answer, and the broader implications of exponentiation, is far more enriching. This article will explore this seemingly simple calculation in depth, covering the fundamental concepts, practical applications, and related mathematical ideas.
Understanding Exponentiation: The Basics
Exponentiation, at its core, is repeated multiplication. When we see an expression like 9⁴, it means we're multiplying 9 by itself four times: 9 x 9 x 9 x 9. The base number (9 in this case) is the number being multiplied, and the exponent (4) indicates how many times the base is multiplied by itself.
Distinguishing between Base and Exponent
It's crucial to understand the difference between the base and the exponent. The base is the number that undergoes the repeated multiplication, while the exponent dictates the number of times this multiplication occurs. Confusing these two will lead to entirely different results.
Calculating 9⁴: The Step-by-Step Approach
Let's break down the calculation of 9⁴ step-by-step to reinforce the concept of repeated multiplication:
-
9 x 9 = 81: Our first multiplication yields 81.
-
81 x 9 = 729: Multiplying the result by 9 again gives us 729.
-
729 x 9 = 6561: Finally, multiplying 729 by 9 results in 6561.
Therefore, 9⁴ = 6561.
Beyond the Calculation: Exploring the Broader Context of Exponentiation
While calculating 9⁴ is relatively simple, understanding the broader implications of exponentiation is crucial for its diverse applications in various fields.
Exponentiation in Different Mathematical Contexts
Exponentiation isn't confined to simple integer calculations. It extends to:
-
Fractional Exponents: Expressions like 9^(1/2) represent the square root of 9 (which is 3). Fractional exponents introduce the concept of roots.
-
Negative Exponents: 9^(-1) is equivalent to 1/9. Negative exponents represent reciprocals.
-
Decimal Exponents: Exponents can be decimals, leading to more complex calculations often requiring calculators or computational tools.
-
Complex Numbers: Exponentiation can even be applied to complex numbers, expanding its reach into advanced mathematical domains.
-
Exponential Functions: In calculus and analysis, exponential functions of the form y = aˣ (where 'a' is a constant) play a fundamental role in modeling various natural phenomena, from population growth to radioactive decay.
Applications of Exponentiation in Real-World Scenarios
The concept of exponentiation isn't just a theoretical exercise; it has practical applications across numerous disciplines:
-
Finance: Compound interest calculations rely heavily on exponentiation. The formula for compound interest involves raising the principal amount to a power determined by the interest rate and time period.
-
Science: Exponential growth and decay are observed in many natural processes. Population growth, radioactive decay, and the spread of diseases can often be modeled using exponential functions.
-
Computer Science: Exponentiation is fundamental to computer algorithms and data structures. Hashing functions, for example, often involve exponentiation. The complexity of many algorithms is expressed using Big O notation, often including exponential terms.
-
Engineering: Many engineering problems, particularly in areas like signal processing and control systems, involve exponential functions and their properties.
Exploring Related Mathematical Concepts
Understanding exponentiation opens doors to other significant mathematical areas:
-
Logarithms: Logarithms are the inverse operation of exponentiation. If 9⁴ = 6561, then the logarithm base 9 of 6561 is 4 (log₉6561 = 4). Logarithms are essential for solving equations involving exponents.
-
Powers of Ten: Understanding powers of ten is critical for working with scientific notation and comprehending very large or very small numbers. Scientific notation uses powers of ten to represent numbers in a concise form.
-
Binomial Theorem: This theorem provides a formula for expanding expressions of the form (a + b)ⁿ, where 'n' is a positive integer. It involves combinations and exponents, highlighting the interconnectedness of various mathematical concepts.
Beyond the Number: The Significance of Understanding Exponentiation
The seemingly simple calculation of 9⁴ illustrates a fundamental concept with far-reaching implications. Understanding exponentiation isn't just about performing calculations; it's about grasping a powerful mathematical tool that underpins many aspects of our world. From the intricacies of financial markets to the complexities of scientific modeling, exponentiation plays a pivotal role.
Developing Mathematical Intuition
Working through problems like calculating 9⁴ helps develop mathematical intuition. It fosters a deeper understanding of numerical relationships and strengthens problem-solving skills. This intuition is invaluable in tackling more complex mathematical challenges.
Connecting Theory to Practice
The ability to connect theoretical mathematical concepts, like exponentiation, to real-world applications is crucial for effective learning. Understanding the practical uses of exponentiation helps solidify the concept and makes it more engaging.
The Power of Continued Learning
Mathematics is a continuously evolving field. The journey of understanding exponentiation serves as a stepping stone to exploring more advanced mathematical concepts and their applications. It encourages a mindset of continuous learning and exploration.
Conclusion: More Than Just a Number
The answer to "What is 9 to the power of 4?" is 6561. But the true value of this question lies in the broader understanding it offers of exponentiation, its diverse applications, and its connection to other mathematical concepts. It underscores the importance of understanding fundamental mathematical principles and their relevance to the world around us. The seemingly simple calculation opens a door to a vast and fascinating world of mathematical possibilities. Continue exploring, continue learning, and continue to be amazed by the power of mathematics.
Latest Posts
Latest Posts
-
How Much Does A Truck Tire Weigh
May 09, 2025
-
How Many Ounces Are In A 1 75 L
May 09, 2025
-
How Much Do A Quarter Of Weed Weigh
May 09, 2025
-
How Many Feet Are In 80 Meters
May 09, 2025
-
Lyrics To I Ve Come Too Far To Look Back
May 09, 2025
Related Post
Thank you for visiting our website which covers about What Is 9 To The Power Of 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.