What Is A 13 Sided Shape Called
Arias News
Mar 30, 2025 · 5 min read
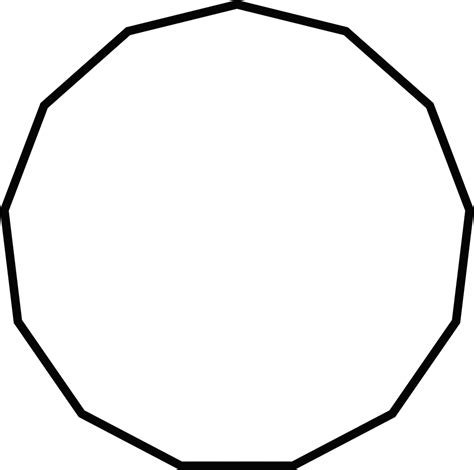
Table of Contents
What is a 13-Sided Shape Called? A Deep Dive into Tridecagons
A 13-sided polygon, a shape with thirteen angles and thirteen sides, is called a tridecagon. While less common than shapes like squares or pentagons, understanding tridecagons opens up a fascinating world of geometry and mathematical exploration. This comprehensive guide delves into the properties, classifications, and interesting facts surrounding this intriguing 13-sided shape.
Understanding Polygons: A Foundation for Tridecagons
Before we fully explore tridecagons, let's establish a fundamental understanding of polygons. Polygons are two-dimensional closed figures composed entirely of straight line segments. These segments are called sides, and the points where the sides meet are called vertices or angles. Polygons are classified based on the number of sides they possess.
- Triangles (3 sides): The simplest polygon.
- Quadrilaterals (4 sides): Includes squares, rectangles, rhombuses, trapezoids, and more.
- Pentagons (5 sides): Often seen in architecture and nature.
- Hexagons (6 sides): Found in honeycombs and various crystals.
- Heptagons (7 sides): Less common but still holds mathematical significance.
- Octagons (8 sides): A classic shape found in stop signs.
- Nonagons (9 sides): Relatively uncommon in everyday life.
- Decagons (10 sides): Represents a significant step in polygon complexity.
- Hendecagons (11 sides): A more obscure polygon.
- Dodecagons (12 sides): Found in some architectural designs.
- Tridecagons (13 sides): Our focus for this article.
- Tetradeccagons (14 sides): And so on...
The Tridecagon: A Deeper Look
The tridecagon, also known as a triskaidecagon (from the Greek words "treis" meaning three, "deka" meaning ten, and "gon" meaning angle), is a polygon with 13 sides and 13 angles. Its name itself highlights its unique position in the world of polygons – a number beyond the commonly encountered shapes.
Properties of a Tridecagon
Like all polygons, tridecagons have specific properties:
- Sum of Interior Angles: The sum of the interior angles of any polygon can be calculated using the formula (n-2) * 180°, where 'n' is the number of sides. For a tridecagon (n=13), the sum of its interior angles is (13-2) * 180° = 1980°.
- Regular vs. Irregular: A regular tridecagon has all sides of equal length and all angles of equal measure (each angle measuring 1980°/13 ≈ 152.31°). An irregular tridecagon has sides and angles of varying lengths and measures.
- Symmetry: A regular tridecagon possesses 13 lines of symmetry, radiating from the center to each vertex, and 13 rotational symmetries. These symmetries contribute to its visually appealing structure.
- Area Calculation: Calculating the area of a regular tridecagon involves more complex formulas compared to simpler polygons. The area can be determined using trigonometric functions based on side length or apothem (the distance from the center to the midpoint of a side).
- Construction: Constructing a precise regular tridecagon using only a compass and straightedge is not possible, as 13 is not a Fermat prime. Approximations are necessary.
Applications and Appearances of Tridecagons
While not as commonly encountered as other polygons, tridecagons can appear in various contexts:
- Tessellations: Although a regular tridecagon cannot tessellate (tile a plane without gaps or overlaps), combinations of tridecagons with other polygons might allow for complex and interesting tessellations.
- Architectural Design: While uncommon, a skilled architect might incorporate a tridecagon into a unique design element, adding an unconventional aesthetic touch.
- Art and Design: Artists and designers might utilize the unique shape to create visually interesting patterns and structures, adding a level of complexity and sophistication.
- Mathematics and Geometry: Tridecagons serve as an excellent tool for teaching and exploring the properties of polygons, especially the complexities encountered with higher-sided shapes. Its unique number of sides leads to interesting mathematical explorations and challenges.
- Nature: While less apparent than other shapes like hexagons, it's possible that approximations of tridecagons could be found in certain natural formations or growth patterns under specific conditions.
Exploring Related Polygons: A Comparative Perspective
Understanding the properties of tridecagons becomes richer when compared to polygons with neighboring numbers of sides:
- Dodecagon (12 sides): The dodecagon is closely related, possessing twelve sides and angles. It's more commonly encountered than the tridecagon, and regular dodecagons can be constructed using a compass and straightedge.
- Tetradeccagon (14 sides): This fourteen-sided polygon is similarly less common than lower-sided polygons. Like the tridecagon, constructing a precise regular tetradeccagon with only compass and straightedge is impossible.
The Mathematical Challenges and Intrigue of Tridecagons
The 13-sided shape presents several mathematical challenges and opportunities for exploration:
- Construction Challenges: The impossibility of constructing a perfect regular tridecagon with compass and straightedge alone highlights the depth of geometric constructions. This limitation underscores the complexities involved in dealing with polygons possessing a prime number of sides.
- Area Calculations: Calculating the area of a tridecagon, especially an irregular one, requires sophisticated mathematical techniques and possibly computational tools.
- Advanced Geometrical Properties: Further exploration into the more complex geometrical properties of the tridecagon, including its angles, side lengths, and relationships to other geometrical figures, offers rich opportunities for mathematical investigation.
Beyond the Basics: Advanced Topics and Further Research
For those interested in a deeper dive into the world of tridecagons and related geometrical concepts, several avenues of exploration exist:
- Non-Euclidean Geometry: Exploring tridecagons within non-Euclidean geometries, such as spherical or hyperbolic geometry, can reveal interesting variations in their properties.
- Computational Geometry: Utilizing computational geometry tools and software can allow for precise calculations and simulations of tridecagons, particularly in complex scenarios or irregular shapes.
- Advanced Mathematical Proofs: Investigating and attempting to prove specific theorems related to tridecagons within the field of geometry can present exciting mathematical challenges.
Conclusion: The Unsung Hero of Polygons
The tridecagon, while often overshadowed by its more frequently encountered polygonal brethren, offers a unique perspective into the intriguing world of geometry and mathematics. Its thirteen sides and angles present a compelling challenge to our understanding of shapes and patterns, prompting further exploration and expanding our mathematical knowledge. From its inherent properties to its potential applications in diverse fields, the tridecagon serves as a reminder of the beauty and complexity found within the seemingly simple world of geometry. Its study offers a rewarding journey for mathematics enthusiasts and curious minds alike. Whether appreciating its visual appeal, delving into its mathematical properties, or exploring its potential in various applications, the tridecagon remains a fascinating shape worthy of continued study and admiration.
Latest Posts
Latest Posts
-
What Do You Call A Person Who Gives Massages
Apr 01, 2025
-
It Aint Over Til Its Over Smokey Robinson
Apr 01, 2025
-
The Quantity Of Matter In An Object
Apr 01, 2025
-
What Year Was I Born If Im 47
Apr 01, 2025
-
How Long Would It Take To Walk 0 3 Miles
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about What Is A 13 Sided Shape Called . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
