What Is A Equivalent Fraction For 2/5
Arias News
Mar 30, 2025 · 5 min read
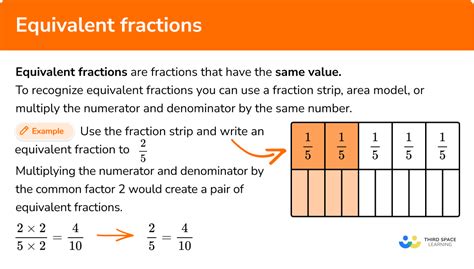
Table of Contents
What is an Equivalent Fraction for 2/5? A Deep Dive into Fraction Equivalence
Finding equivalent fractions is a fundamental concept in mathematics, crucial for understanding fractions, simplifying expressions, and solving various problems. This comprehensive guide delves into the meaning of equivalent fractions, focusing specifically on finding equivalent fractions for 2/5. We'll explore different methods, provide numerous examples, and discuss the importance of this concept in various mathematical contexts.
Understanding Equivalent Fractions
Equivalent fractions represent the same proportion or value, even though they appear different. They share the same ratio, meaning the numerator (the top number) and the denominator (the bottom number) are proportionally related. Imagine slicing a pizza: half a pizza (1/2) is the same as two quarters (2/4) or four eighths (4/8). These are all equivalent fractions.
Key Principle: To obtain an equivalent fraction, you must multiply or divide both the numerator and the denominator by the same non-zero number. This ensures that the ratio remains constant. Multiplying by a number is essentially increasing the number of slices while maintaining the same portion of the whole. Dividing decreases the number of slices while keeping the same proportion.
Methods for Finding Equivalent Fractions of 2/5
Let's focus specifically on finding equivalent fractions for 2/5. We can achieve this using two main methods:
1. Multiplying the Numerator and Denominator
This is the most common approach. Choose any non-zero integer, and multiply both the numerator (2) and the denominator (5) by that number. This will generate an equivalent fraction.
Examples:
- Multiply by 2: (2 x 2) / (5 x 2) = 4/10
- Multiply by 3: (2 x 3) / (5 x 3) = 6/15
- Multiply by 4: (2 x 4) / (5 x 4) = 8/20
- Multiply by 5: (2 x 5) / (5 x 5) = 10/25
- Multiply by 10: (2 x 10) / (5 x 10) = 20/50
- Multiply by 100: (2 x 100) / (5 x 100) = 200/500
As you can see, we can generate an infinite number of equivalent fractions for 2/5 by simply multiplying both the numerator and denominator by different integers. All these fractions, 4/10, 6/15, 8/20, 10/25, 20/50, 200/500, etc., represent the same portion or value as 2/5.
2. Simplifying Fractions (Finding Equivalent Fractions in Lowest Terms)
Sometimes you might encounter a fraction that is equivalent to 2/5 but is not in its simplest form. Simplifying a fraction involves dividing both the numerator and denominator by their greatest common divisor (GCD). The GCD is the largest number that divides both the numerator and the denominator without leaving a remainder.
Let's say we have the fraction 20/50. To simplify it:
- Find the GCD of 20 and 50: The GCD of 20 and 50 is 10.
- Divide both the numerator and the denominator by the GCD: 20 ÷ 10 = 2 and 50 ÷ 10 = 5.
Therefore, the simplified fraction is 2/5, confirming that 20/50 is an equivalent fraction. This process is crucial for representing fractions in their most concise and manageable form.
Applications of Equivalent Fractions
Understanding and working with equivalent fractions is essential in numerous mathematical applications:
1. Adding and Subtracting Fractions
To add or subtract fractions, they must have a common denominator. Finding equivalent fractions allows you to rewrite fractions with different denominators into fractions with the same denominator, facilitating the addition or subtraction process.
Example: Adding 2/5 and 1/10. We can convert 2/5 to its equivalent fraction 4/10, then add 4/10 + 1/10 = 5/10, which simplifies to 1/2.
2. Comparing Fractions
Determining which fraction is larger or smaller requires comparing them with a common denominator. Equivalent fractions allow us to convert the fractions into a comparable form.
Example: Comparing 2/5 and 3/7. Finding common denominators (e.g., 35) and converting the fractions to equivalent fractions (14/35 and 15/35) allows us to see that 3/7 is larger than 2/5.
3. Solving Equations
Many algebraic equations involve fractions. Understanding equivalent fractions is crucial for manipulating and solving these equations. This includes simplifying complex expressions and isolating variables.
4. Real-World Applications
Equivalent fractions find practical applications in everyday life:
- Cooking and Baking: Recipes often use fractions. Understanding equivalent fractions allows for adjustments to recipe quantities.
- Measurement: Converting between different units of measurement frequently involves using equivalent fractions.
- Construction and Engineering: Precise measurements and calculations are crucial, and equivalent fractions often play a key role.
Beyond the Basics: Exploring More Complex Scenarios
While multiplying and dividing by whole numbers is the most straightforward method, you can also use decimals and even algebraic expressions to generate equivalent fractions.
Using Decimals
You can multiply both the numerator and denominator of 2/5 by a decimal. For example, multiplying by 0.5 gives (2 * 0.5) / (5 * 0.5) = 1/2.5. While this is mathematically correct, it's generally preferred to work with whole numbers to avoid complications.
Using Algebraic Expressions
This is more advanced and is used in higher-level mathematics. The principle remains the same: multiply the numerator and denominator by the same algebraic expression. For example, multiplying by 'x' gives (2x)/(5x). This is still equivalent to 2/5 as long as x is not zero.
Conclusion: Mastering Equivalent Fractions
The ability to identify and work with equivalent fractions is a cornerstone of mathematical proficiency. Understanding the concept of equivalent fractions—that they represent the same proportion even with different numerators and denominators—is crucial for solving a wide variety of problems. The methods discussed here—multiplying and dividing both the numerator and denominator by the same non-zero number—form the basis for manipulating fractions effectively in numerous mathematical contexts, from simple arithmetic to more advanced algebraic manipulations and real-world applications. Mastering this fundamental concept will greatly enhance your mathematical skills and problem-solving abilities. Remember, practice is key! The more you work with fractions, the more comfortable and proficient you will become.
Latest Posts
Latest Posts
-
Cars That Start With The Letter T
Apr 01, 2025
-
Is The Name Jack In The Bible
Apr 01, 2025
-
How Many Times Does 5 Go Into 100
Apr 01, 2025
-
Is 11 16 Bigger Than 3 4
Apr 01, 2025
-
How Many Feet Is 1 3 Acre
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about What Is A Equivalent Fraction For 2/5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
