What Is Bigger 3 8 Or 5 16
Arias News
May 10, 2025 · 4 min read
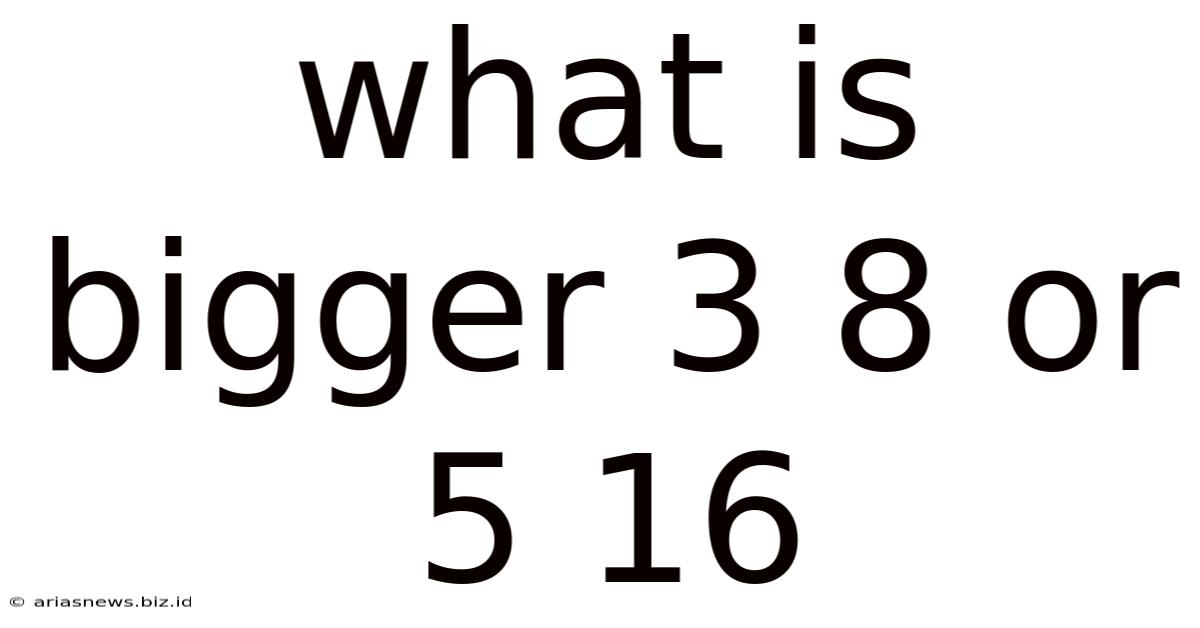
Table of Contents
What's Bigger: 3/8 or 5/16? A Deep Dive into Fraction Comparison
Comparing fractions might seem like elementary school math, but understanding the underlying principles is crucial for various applications, from baking to advanced engineering. This article tackles the seemingly simple question: What's bigger: 3/8 or 5/16? We'll go beyond simply providing the answer; we'll explore multiple methods to compare fractions, explain the reasoning behind each, and delve into the broader context of fraction manipulation. This comprehensive guide will equip you with the skills to confidently compare any two fractions.
Understanding Fractions: A Quick Refresher
Before we tackle the comparison, let's briefly review what fractions represent. A fraction, like 3/8, consists of two main parts:
- Numerator: The top number (3 in this case) represents the number of parts you have.
- Denominator: The bottom number (8 in this case) represents the total number of equal parts the whole is divided into.
Therefore, 3/8 represents 3 out of 8 equal parts of a whole. Similarly, 5/16 represents 5 out of 16 equal parts.
Method 1: Finding a Common Denominator
The most straightforward method for comparing fractions is to find a common denominator. This involves finding a number that is a multiple of both denominators (8 and 16 in our case). Since 16 is a multiple of 8 (8 x 2 = 16), we can easily convert 3/8 to have a denominator of 16.
To do this, we multiply both the numerator and the denominator of 3/8 by 2:
(3 x 2) / (8 x 2) = 6/16
Now we can directly compare 6/16 and 5/16. Since 6 is greater than 5, we can conclude that 6/16 (or 3/8) is bigger than 5/16.
Why This Method Works
This method works because it allows us to express both fractions in terms of the same unit of measurement. By converting both fractions to have the same denominator, we're essentially comparing the same-sized pieces. It's like comparing apples to apples instead of apples to oranges.
Method 2: Converting to Decimals
Another effective method is to convert both fractions into decimals. This involves dividing the numerator by the denominator for each fraction.
- 3/8 = 0.375
- 5/16 = 0.3125
Comparing the decimal values, we see that 0.375 is greater than 0.3125. Therefore, 3/8 is bigger than 5/16.
Why This Method Works
Converting to decimals provides a clear numerical comparison. Decimals are easy to understand and compare, especially when dealing with fractions that don't share an easily identifiable common denominator. This method is particularly useful when using calculators or computer programs.
Method 3: Visual Representation
While less precise for complex fractions, visualizing the fractions can provide an intuitive understanding. Imagine two identical pies. Divide one pie into 8 equal slices and take 3 slices (3/8). Divide the other pie into 16 equal slices and take 5 slices (5/16). Visually comparing the portions of pie, it becomes clear that 3/8 represents a larger portion than 5/16.
Why This Method Works
Visual representation is a powerful tool for grasping the concept of fractions, especially for beginners. It makes abstract concepts concrete and relatable, fostering a deeper understanding of fractional values. However, this method is less practical for comparing fractions with larger or less easily visualized denominators.
Expanding the Understanding: More Complex Fraction Comparisons
The principles applied above can be extended to compare any two fractions, no matter how complex they appear. Let's consider a more challenging example: comparing 7/12 and 11/18.
To find a common denominator, we need to find the least common multiple (LCM) of 12 and 18. The LCM of 12 and 18 is 36.
- Converting 7/12: (7 x 3) / (12 x 3) = 21/36
- Converting 11/18: (11 x 2) / (18 x 2) = 22/36
Now, we can see that 22/36 > 21/36, meaning 11/18 is bigger than 7/12.
Similarly, converting to decimals would yield:
- 7/12 ≈ 0.583
- 11/18 ≈ 0.611
Again, 0.611 > 0.583, confirming that 11/18 is larger.
Practical Applications of Fraction Comparison
The ability to compare fractions isn't just an academic exercise. It has practical applications across many fields:
- Cooking and Baking: Recipes often involve fractions of ingredients. Knowing how to compare fractions ensures you use the correct amounts.
- Construction and Engineering: Precise measurements are crucial in these fields, and comparing fractions is essential for accurate calculations and designs.
- Data Analysis: Fractions frequently appear in data representation and statistical calculations. Understanding fraction comparison is vital for interpreting data correctly.
- Finance: Fractions are used in many financial calculations, such as calculating interest rates and proportions of investments.
Conclusion: Mastering Fraction Comparison
Comparing fractions, while seemingly simple, is a fundamental mathematical skill with wide-ranging applications. By mastering the techniques of finding common denominators, converting to decimals, and using visual representations, you can confidently tackle any fraction comparison problem. This comprehensive understanding empowers you to approach various tasks with precision and accuracy, enhancing your problem-solving abilities across numerous disciplines. Remember, the key lies in understanding the underlying principles – the rest is just practice and application!
Latest Posts
Latest Posts
-
How Many 1 4 Teaspoons Make 3 4 Teaspoon
May 10, 2025
-
How Many Milliliters Are In A Half Pint
May 10, 2025
-
Is Peter Firth Related To Colin Firth
May 10, 2025
-
If Your 40 What Year Was You Born
May 10, 2025
-
How Long Is 168 Hours In Days
May 10, 2025
Related Post
Thank you for visiting our website which covers about What Is Bigger 3 8 Or 5 16 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.