What Is Half Of 1 3 4 Cups
Arias News
May 12, 2025 · 4 min read
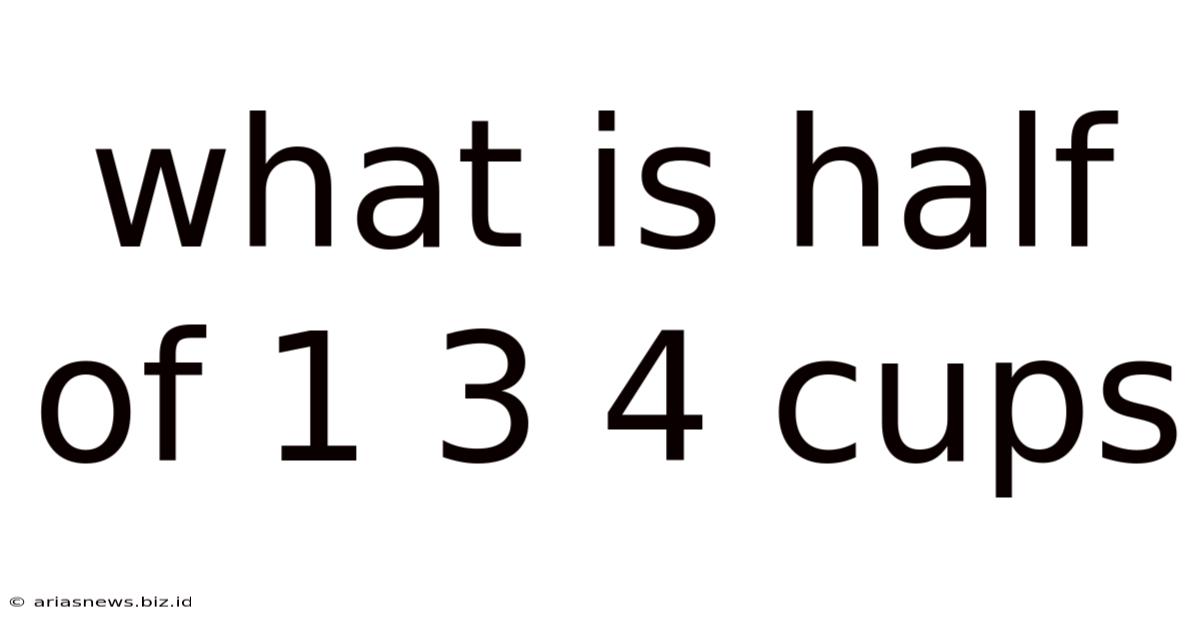
Table of Contents
What is Half of 1 3/4 Cups? A Comprehensive Guide to Fraction Division
This seemingly simple question, "What is half of 1 3/4 cups?", opens the door to a deeper understanding of fractions, a crucial skill in many aspects of life, from baking and cooking to construction and engineering. While a quick calculation might suffice for some, this article delves into the various methods of solving this problem, explains the underlying mathematical principles, and explores practical applications to solidify your understanding. We'll cover everything from basic fraction manipulation to real-world examples, ensuring you become confident in tackling similar problems in the future.
Understanding Fractions: A Quick Refresher
Before diving into the solution, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's composed of two parts: the numerator (the top number) and the denominator (the bottom number). The numerator indicates how many parts we have, while the denominator indicates how many equal parts the whole is divided into.
In our case, we have the mixed number 1 3/4. This represents one whole and three-quarters of another. To perform calculations, it's often easier to convert mixed numbers into improper fractions.
Converting Mixed Numbers to Improper Fractions
Converting 1 3/4 to an improper fraction involves these steps:
- Multiply the whole number by the denominator: 1 * 4 = 4
- Add the numerator to the result: 4 + 3 = 7
- Keep the same denominator: 4
Therefore, 1 3/4 is equivalent to 7/4.
Calculating Half of 1 3/4 Cups: Method 1 - Using Improper Fractions
Now that we have our improper fraction, we can calculate half of it. Finding half of a number is the same as dividing it by 2 or multiplying it by 1/2. Let's use the multiplication method:
(7/4) * (1/2) = 7/8
Therefore, half of 1 3/4 cups is 7/8 cups.
Calculating Half of 1 3/4 Cups: Method 2 - Halving the Whole and the Fraction Separately
Alternatively, we can halve the whole number and the fractional part separately.
- Halve the whole number: 1 / 2 = 1/2
- Halve the fraction: (3/4) / 2 = 3/8
- Add the results: 1/2 + 3/8 = 4/8 + 3/8 = 7/8
Again, we arrive at the answer: 7/8 cups. This method demonstrates the flexibility of working with fractions and offers a visual understanding of the process.
Practical Applications: Recipes and Everyday Life
Understanding fraction division is invaluable in various real-world scenarios. Imagine you're baking a cake and the recipe calls for 1 3/4 cups of flour, but you only want to make half the recipe. Knowing that half of 1 3/4 cups is 7/8 cups ensures you get the correct amount of flour, leading to a perfectly baked cake.
This skill isn't limited to baking. Consider these examples:
- Cooking: Adjusting recipe portions for different numbers of servings.
- Construction: Calculating material quantities for projects.
- Sewing: Determining fabric requirements for garments.
- Gardening: Measuring fertilizer or pesticide amounts.
- Finance: Calculating proportions of investments or budgets.
Beyond the Basics: Working with More Complex Fractions
While our example involved a relatively simple fraction, the principles remain the same when dealing with more complex calculations. For example, what if the recipe called for 2 5/8 cups of sugar and you wanted to make a quarter of the recipe? The process involves the same steps:
- Convert to an improper fraction: 2 5/8 = 21/8
- Multiply by the fraction representing the desired portion: (21/8) * (1/4) = 21/32
This highlights the importance of mastering fraction manipulation. Practice regularly with different examples to build confidence and accuracy.
Tips for Mastering Fraction Division
- Practice regularly: The key to mastering any mathematical concept is consistent practice. Start with simple problems and gradually increase the complexity.
- Visual aids: Using diagrams or visual representations of fractions can help solidify understanding.
- Online resources: Numerous online resources, such as educational websites and videos, offer further explanation and practice exercises.
- Seek help when needed: Don't hesitate to ask for help from teachers, tutors, or peers if you're struggling with any aspect of fraction division.
Conclusion: Half a Cup, a World of Possibilities
The seemingly simple task of finding half of 1 3/4 cups opens the door to a deeper appreciation of fractions and their importance in various contexts. By mastering fraction division, you equip yourself with a valuable skill applicable across numerous fields. Remember, consistent practice and a solid understanding of the underlying principles will pave the way for success in tackling even more complex mathematical challenges. The ability to accurately calculate fractions directly translates to more precise outcomes in cooking, construction, sewing, and countless other areas. So, next time you encounter a fraction-related problem, remember the steps outlined here and confidently approach the solution. You’ll find that the seemingly small act of understanding what’s half of 1 3/4 cups can unlock a world of practical and mathematical possibilities.
Latest Posts
Latest Posts
-
How To Address A Letter To A Nursing Home Resident
May 12, 2025
-
Can Bearded Dragons Eat Brussel Sprout Leaves
May 12, 2025
-
How Many Right Angles Does Trapezoid Have
May 12, 2025
-
Kohler 52 50 02 S Cross Reference
May 12, 2025
-
How Much Is 1 Acre Of Land In Mexico
May 12, 2025
Related Post
Thank you for visiting our website which covers about What Is Half Of 1 3 4 Cups . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.