What Is Half Of 3 And 1/4
Arias News
May 10, 2025 · 4 min read
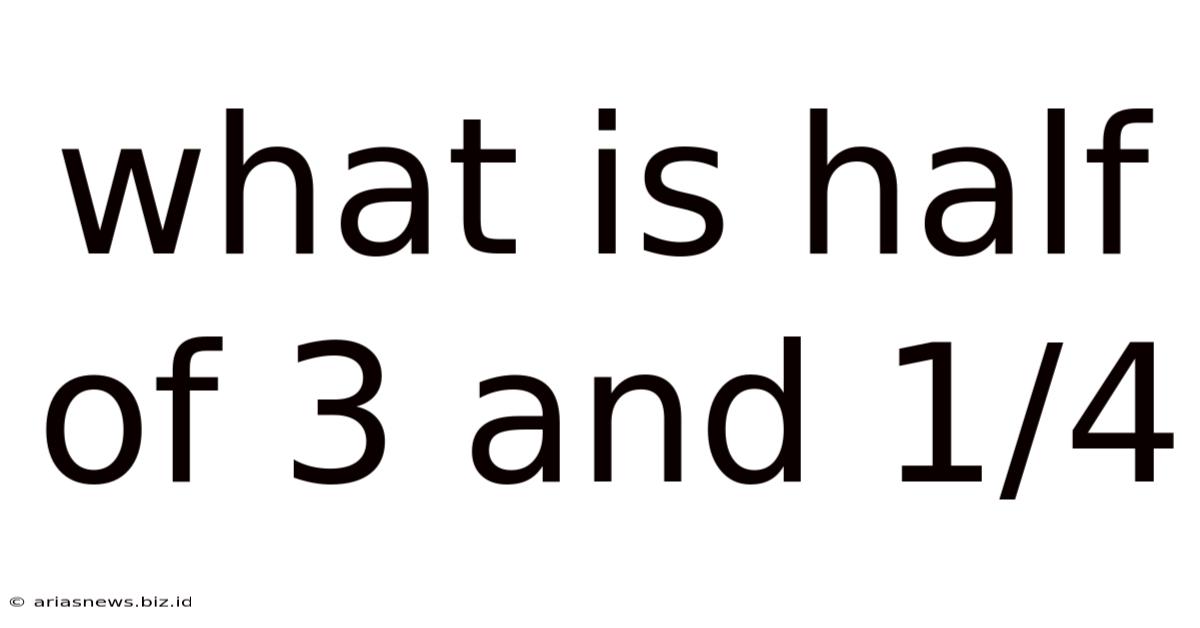
Table of Contents
What is Half of 3 and 1/4? A Comprehensive Guide to Fraction Division
This seemingly simple question, "What is half of 3 and 1/4?", opens the door to a deeper understanding of fractions and division. While the answer might seem straightforward for some, mastering the process involves a solid grasp of fractional representation, conversion techniques, and the mechanics of division. This comprehensive guide will walk you through various methods of solving this problem, reinforcing the underlying mathematical concepts and offering practical applications.
Understanding the Problem: Deconstructing "Half of 3 and 1/4"
Before diving into the solution, let's break down the question itself. The phrase "half of 3 and 1/4" essentially translates to finding one-half (1/2) multiplied by the mixed number 3 and 1/4. This problem combines whole numbers and fractions, requiring a clear understanding of how to work with these different number types. We'll explore different approaches to tackle this, ranging from visual representations to algebraic solutions.
Method 1: Converting to Improper Fractions
This is arguably the most efficient method for solving this type of problem. It involves converting the mixed number (3 and 1/4) into an improper fraction, then performing the multiplication.
Step 1: Converting the Mixed Number
The mixed number 3 and 1/4 represents 3 whole units plus 1/4 of a unit. To convert this to an improper fraction, we multiply the whole number (3) by the denominator of the fraction (4), add the numerator (1), and keep the same denominator (4). This gives us:
(3 * 4) + 1 = 13
Therefore, 3 and 1/4 is equivalent to 13/4.
Step 2: Performing the Multiplication
Now we can rewrite the problem as: (1/2) * (13/4). Multiplying fractions involves multiplying the numerators together and the denominators together:
(1 * 13) / (2 * 4) = 13/8
Step 3: Simplifying the Result
The resulting improper fraction, 13/8, can be converted back into a mixed number by dividing the numerator (13) by the denominator (8):
13 ÷ 8 = 1 with a remainder of 5
This means 13/8 is equivalent to 1 and 5/8.
Therefore, half of 3 and 1/4 is 1 and 5/8.
Method 2: Using Decimal Representation
This method involves converting both the fraction and the mixed number into their decimal equivalents, then performing the multiplication.
Step 1: Converting to Decimals
The fraction 1/2 is equivalent to 0.5. The mixed number 3 and 1/4 can be converted to a decimal by dividing 1 by 4 (0.25) and adding this to 3, resulting in 3.25.
Step 2: Performing the Multiplication
Now we can rewrite the problem as 0.5 * 3.25. Performing this multiplication yields:
0.5 * 3.25 = 1.625
Step 3: Converting back to a Fraction (Optional)
While the decimal answer is perfectly valid, it can be converted back to a fraction if needed. 1.625 can be written as 1 and 625/1000. Simplifying this fraction by dividing both the numerator and denominator by their greatest common divisor (125) gives us:
625/1000 = 5/8
This confirms that 1.625 is equivalent to 1 and 5/8.
Method 3: Visual Representation (for Conceptual Understanding)
While not the most efficient method for calculations, visualizing the problem can enhance understanding, particularly for beginners. Imagine a rectangle representing 3 and 1/4 units. To find half of this, you would divide the rectangle into two equal halves. Each half would then represent 1 and 13/8 units. This visual representation solidifies the concept of dividing a mixed number by two.
Applications and Real-World Examples
Understanding fraction division extends beyond classroom exercises. It's applicable in numerous everyday situations:
- Cooking: Halving or doubling recipes often involves working with fractions and mixed numbers. If a recipe calls for 3 and 1/4 cups of flour and you want to halve it, you'll need to calculate half of 3 and 1/4.
- Construction: Measuring and cutting materials often requires precise fractional calculations.
- Sewing and Crafting: Pattern adjustments and material estimations frequently involve working with fractions.
- Finance: Calculating portions of investments or determining interest often involves fractions and decimals.
Advanced Concepts and Further Exploration
This problem serves as a stepping stone to more complex fractional calculations. Consider exploring the following concepts to deepen your understanding:
- Dividing by fractions: Understanding that dividing by a fraction is the same as multiplying by its reciprocal.
- Complex fractions: Working with fractions within fractions.
- Solving equations involving fractions: Applying fraction operations within algebraic equations.
Conclusion: Mastering Fraction Division
The question "What is half of 3 and 1/4?" might seem simple at first glance, but its solution unveils the importance of mastering fractional arithmetic. By exploring different methods—converting to improper fractions, using decimals, or even visualizing the problem—we’ve demonstrated a thorough understanding of the underlying mathematical principles. Remember, proficiency in fraction division is a valuable skill with numerous real-world applications. Continue practicing these methods, and you'll find yourself confidently tackling increasingly complex mathematical challenges. The journey of mastering fractions is one of continuous learning and practical application, ultimately rewarding you with a strengthened mathematical foundation.
Latest Posts
Latest Posts
-
How Do You Measure The Wheelbase On A Semi Truck
May 10, 2025
-
A Refrigerant Oil That Is Hygroscopic Is
May 10, 2025
-
How Many Bottles Of Water Equal A Liter
May 10, 2025
-
How Much Does 64 Ounces Of Water Weigh
May 10, 2025
-
How Many Degrees Celsius Is 400 Degrees Fahrenheit
May 10, 2025
Related Post
Thank you for visiting our website which covers about What Is Half Of 3 And 1/4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.