What Is One Half As A Percentage
Arias News
May 11, 2025 · 5 min read
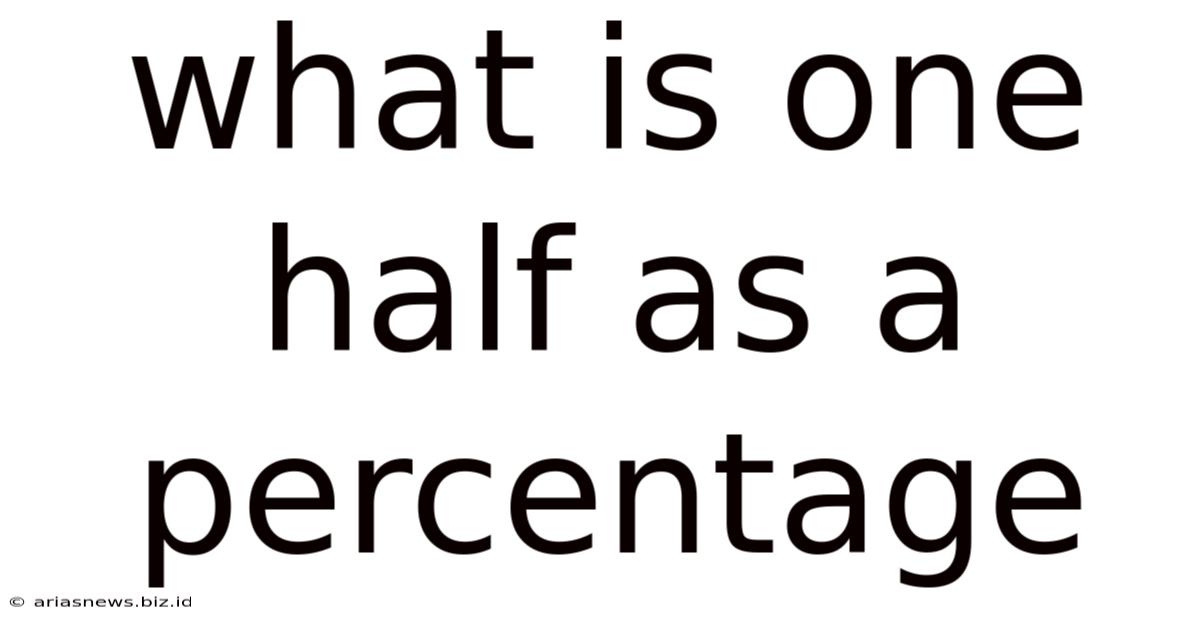
Table of Contents
What is One Half as a Percentage? A Comprehensive Guide
Understanding fractions and their percentage equivalents is fundamental to many aspects of life, from calculating discounts in a store to understanding financial reports. This comprehensive guide will explore the concept of one-half as a percentage, delving into the methods for conversion, practical applications, and related concepts to solidify your understanding.
Understanding Fractions and Percentages
Before we dive into the specifics of one-half, let's establish a clear understanding of fractions and percentages.
Fractions: A fraction represents a part of a whole. It consists of two numbers: a numerator (the top number) and a denominator (the bottom number). The numerator indicates the number of parts you have, while the denominator indicates the total number of parts the whole is divided into. For example, ½ means you have one part out of a total of two parts.
Percentages: A percentage is a way of expressing a number as a fraction of 100. The symbol "%" represents "per cent," which literally means "out of one hundred." Percentages are widely used because they provide a standardized way to compare different fractions or proportions.
Converting One-Half to a Percentage
The conversion of one-half (½) to a percentage involves two simple steps:
Step 1: Convert the fraction to a decimal.
To convert a fraction to a decimal, you divide the numerator by the denominator. In the case of ½:
1 ÷ 2 = 0.5
Step 2: Convert the decimal to a percentage.
To convert a decimal to a percentage, you multiply the decimal by 100 and add the "%" symbol. Therefore:
0.5 x 100 = 50%
Therefore, one-half is equal to 50%.
Alternative Methods for Conversion
While the method described above is the most straightforward, there are other approaches you can use to convert one-half to a percentage:
Method 1: Using Proportions:
You can set up a proportion to solve for the percentage:
½ = x/100
Cross-multiplying gives:
2x = 100
x = 50
Therefore, x = 50%, confirming that one-half is 50%.
Method 2: Understanding the Relationship between Fractions and Percentages:
Recognizing that percentages are essentially fractions with a denominator of 100 can simplify the conversion. Since ½ is equivalent to 50/100 (because you can multiply both numerator and denominator by 50), it directly translates to 50%. This method highlights the inherent connection between fractions and percentages.
Practical Applications of One-Half as a Percentage (50%)
The concept of 50% finds widespread use in numerous real-world scenarios:
-
Sales and Discounts: A 50% discount means you pay half the original price. If an item costs $100, a 50% discount reduces the price to $50.
-
Statistics and Probability: In probability, a 50% chance indicates an even likelihood of an event occurring. For example, flipping a fair coin has a 50% chance of landing on heads.
-
Financial Calculations: Understanding 50% is crucial for calculating interest rates, profit margins, and other financial metrics. For example, if a company makes a 50% profit margin, it means that half of its revenue is profit.
-
Data Analysis: Representing data using percentages often makes it easier to understand and interpret. Showing that 50% of respondents agree with a particular survey question gives a clear visual representation of the data.
-
Everyday Calculations: Dividing something equally between two people is the same as calculating 50% for each person.
Beyond One-Half: Working with Other Fractions and Percentages
While this guide focuses on one-half, understanding the principles of fraction-to-percentage conversion extends to all fractions. Here's a brief overview:
-
Converting any fraction to a percentage: Always divide the numerator by the denominator to get a decimal, then multiply by 100 to obtain the percentage.
-
Converting a percentage to a fraction: Divide the percentage by 100 and simplify the resulting fraction. For example, 75% becomes 75/100, which simplifies to ¾.
-
Working with mixed numbers: Convert mixed numbers (like 1 ½) into improper fractions (like 3/2) before converting to a decimal and then a percentage.
-
Using a calculator: Calculators greatly simplify the conversion process, especially for more complex fractions.
Common Percentage Equivalents to Know:
Learning common fraction-percentage equivalents can significantly speed up your calculations and improve your understanding of proportions. Here are a few examples:
- 1/4 = 25%
- 1/3 ≈ 33.33%
- 2/3 ≈ 66.67%
- 3/4 = 75%
- 1/5 = 20%
- 1/10 = 10%
Troubleshooting Common Mistakes:
-
Forgetting to multiply by 100: A common error is to stop at the decimal stage, failing to multiply by 100 to obtain the percentage.
-
Incorrectly simplifying fractions: Ensure fractions are simplified correctly before conversion to avoid inaccuracies.
-
Misunderstanding decimal places: Pay close attention to decimal places during division and multiplication to ensure accuracy.
Conclusion: Mastering Percentages is Key
Understanding the concept of one-half as a percentage, and more generally, how to convert between fractions and percentages, is a vital skill for various aspects of daily life and professional endeavors. By mastering these fundamental concepts and applying the methods outlined in this guide, you'll significantly improve your mathematical abilities and enhance your problem-solving skills. Remember to practice regularly and use different methods to reinforce your understanding. The more you practice, the more comfortable and confident you'll become in tackling percentage-related problems. This mastery will enable you to confidently navigate financial transactions, interpret data, and solve problems in various contexts with ease and accuracy. So, embrace the power of percentages, and unlock a world of numerical understanding!
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is One Half As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.