What Is The Gcf For 15 And 20
Arias News
Mar 29, 2025 · 5 min read
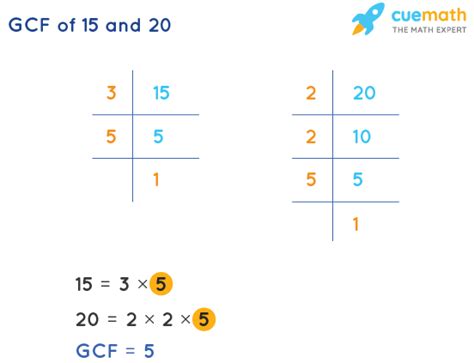
Table of Contents
What is the GCF for 15 and 20? A Deep Dive into Finding the Greatest Common Factor
Finding the greatest common factor (GCF) might seem like a simple arithmetic task, but understanding the underlying principles and exploring various methods to solve it can significantly enhance your mathematical understanding and problem-solving skills. This comprehensive guide will delve deep into determining the GCF for 15 and 20, exploring multiple approaches, and demonstrating their applicability to broader scenarios. We'll also touch upon the practical applications of GCF in various fields.
Understanding the Greatest Common Factor (GCF)
The Greatest Common Factor (GCF), also known as the Greatest Common Divisor (GCD), is the largest positive integer that divides each of the integers without leaving a remainder. In simpler terms, it's the biggest number that perfectly divides both numbers. Understanding this definition is crucial before we begin calculating the GCF for 15 and 20.
Why is GCF Important?
The GCF has numerous applications across various fields:
-
Simplification of Fractions: The GCF is fundamental in simplifying fractions to their lowest terms. Dividing both the numerator and denominator by their GCF results in an equivalent fraction in its simplest form.
-
Algebraic Expressions: GCF is essential when simplifying algebraic expressions by factoring out common terms.
-
Geometry and Measurement: GCF is used in solving problems related to area, perimeter, and volume, particularly when dealing with dimensions that need to be broken down into smaller, equal parts.
-
Real-World Applications: GCF finds applications in scenarios involving dividing quantities into equal groups or finding the largest possible size of identical items that can be created from a given set of materials.
Methods for Finding the GCF of 15 and 20
Several methods can be employed to determine the GCF of 15 and 20. Let's explore the most common ones:
1. Listing Factors Method
This method involves listing all the factors of each number and then identifying the largest common factor.
Factors of 15: 1, 3, 5, 15 Factors of 20: 1, 2, 4, 5, 10, 20
Comparing the two lists, we see that the common factors are 1 and 5. The greatest of these common factors is 5. Therefore, the GCF of 15 and 20 is 5.
This method is straightforward for smaller numbers but can become cumbersome when dealing with larger numbers with many factors.
2. Prime Factorization Method
This method involves finding the prime factorization of each number and then identifying the common prime factors raised to the lowest power.
Prime Factorization of 15: 3 x 5 Prime Factorization of 20: 2 x 2 x 5 (or 2² x 5)
The common prime factor is 5. Since it appears only once in the factorization of 15 (and once in 20), the GCF is simply 5.
This method is more efficient for larger numbers as it systematically breaks down the numbers into their prime components.
3. Euclidean Algorithm
The Euclidean algorithm is a highly efficient method, particularly for larger numbers. It uses a repetitive division process.
- Divide the larger number (20) by the smaller number (15): 20 ÷ 15 = 1 with a remainder of 5.
- Replace the larger number with the smaller number (15) and the smaller number with the remainder (5): 15 ÷ 5 = 3 with a remainder of 0.
- Since the remainder is 0, the GCF is the last non-zero remainder, which is 5.
The Euclidean algorithm is elegant in its simplicity and efficiency, especially when dealing with large numbers where listing factors or prime factorization becomes impractical.
Extending the Concept: GCF of More Than Two Numbers
The methods described above can be extended to find the GCF of more than two numbers. Let's find the GCF of 15, 20, and 30 using the prime factorization method:
Prime Factorization of 15: 3 x 5 Prime Factorization of 20: 2² x 5 Prime Factorization of 30: 2 x 3 x 5
The common prime factors are 5. Therefore, the GCF of 15, 20, and 30 is 5.
Practical Applications: Real-World Examples
Let's explore some real-world scenarios where understanding GCF is beneficial:
Scenario 1: Dividing Candy
You have 15 chocolate bars and 20 gummy bears. You want to divide them equally among your friends without any leftovers. The GCF (5) tells you the maximum number of friends you can have, where each friend receives 3 chocolate bars and 4 gummy bears.
Scenario 2: Tiling a Floor
You need to tile a rectangular floor with dimensions 15 feet by 20 feet. You want to use square tiles of the largest possible size. The GCF (5) indicates that the largest square tile you can use is 5 feet by 5 feet.
Scenario 3: Simplifying Fractions
The fraction 15/20 can be simplified by dividing both the numerator and denominator by their GCF (5), resulting in the equivalent fraction 3/4.
Conclusion: Mastering the GCF
Finding the greatest common factor is a fundamental concept in mathematics with wide-ranging applications. While the listing factors method is intuitive for small numbers, the prime factorization and Euclidean algorithm offer more efficient solutions for larger numbers. Understanding these methods empowers you to solve various problems efficiently and effectively, from simplifying fractions to optimizing real-world tasks involving division and measurement. Mastering the GCF enhances your mathematical skills and provides valuable tools for problem-solving across diverse fields. Remember to choose the method that best suits the numbers you're working with for optimal efficiency.
Latest Posts
Latest Posts
-
How Far Can The Dog Run Into The Woods
Mar 31, 2025
-
A Drawing That Shows Information Like A Graph
Mar 31, 2025
-
How Much Do Deadliest Catch Crew Make Per Episode
Mar 31, 2025
-
How Many Feet In A Story Of A Building
Mar 31, 2025
-
How To Beat Level 27 On 40x Escape
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about What Is The Gcf For 15 And 20 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
