What Is The Gcf For 18 And 30
Arias News
Apr 08, 2025 · 6 min read
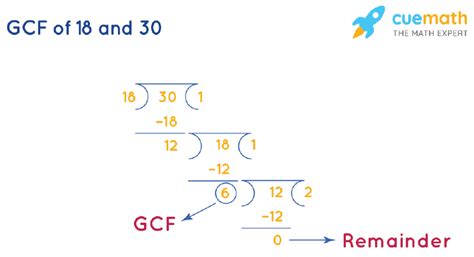
Table of Contents
What is the GCF for 18 and 30? A Deep Dive into Greatest Common Factors
Finding the greatest common factor (GCF) might seem like a simple arithmetic task, but understanding the underlying principles and exploring different methods can significantly enhance your mathematical understanding and problem-solving skills. This comprehensive guide delves into the question, "What is the GCF for 18 and 30?", providing multiple approaches to finding the solution and expanding on the broader concept of GCFs. We'll move beyond simply stating the answer and explore the why behind the calculations, making this a valuable resource for students and anyone seeking to solidify their grasp on number theory.
Understanding Greatest Common Factors (GCF)
Before jumping into the specifics of 18 and 30, let's establish a solid foundation. The greatest common factor (GCF), also known as the greatest common divisor (GCD), is the largest positive integer that divides each of the integers without leaving a remainder. In simpler terms, it's the biggest number that goes into both numbers evenly.
Why are GCFs important? GCFs are fundamental in various mathematical applications, including:
- Simplifying fractions: Finding the GCF of the numerator and denominator allows you to reduce a fraction to its simplest form.
- Algebraic manipulations: GCFs are crucial in factoring polynomials and simplifying algebraic expressions.
- Real-world applications: GCF concepts appear in various real-world scenarios, such as dividing items into equal groups or determining the size of the largest square tile that can perfectly cover a rectangular area.
Method 1: Listing Factors
The most straightforward approach to finding the GCF is by listing all the factors of each number and then identifying the largest common factor.
Factors of 18: 1, 2, 3, 6, 9, 18
Factors of 30: 1, 2, 3, 5, 6, 10, 15, 30
By comparing the two lists, we can see the common factors are 1, 2, 3, and 6. The greatest of these common factors is 6. Therefore, the GCF of 18 and 30 is 6.
This method is effective for smaller numbers, but it becomes less efficient as the numbers increase in size.
Method 2: Prime Factorization
Prime factorization is a more systematic and powerful method, especially for larger numbers. It involves expressing each number as a product of its prime factors. A prime number is a whole number greater than 1 that has only two divisors: 1 and itself (e.g., 2, 3, 5, 7, 11...).
Prime factorization of 18: 2 x 3 x 3 = 2 x 3²
Prime factorization of 30: 2 x 3 x 5
Now, identify the common prime factors and their lowest powers:
- Both numbers share a factor of 2 (to the power of 1).
- Both numbers share a factor of 3 (to the power of 1).
Multiply the common prime factors together: 2 x 3 = 6
Therefore, the GCF of 18 and 30 is 6.
This method is more efficient than listing factors, especially when dealing with larger numbers because it provides a structured approach to identifying common factors.
Method 3: Euclidean Algorithm
The Euclidean algorithm is a highly efficient method for finding the GCF of two numbers, especially large ones. It's based on the principle that the GCF of two numbers does not change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal, and that number is the GCF.
Let's apply the Euclidean algorithm to 18 and 30:
- Step 1: Subtract the smaller number (18) from the larger number (30): 30 - 18 = 12
- Step 2: Now, we have the numbers 18 and 12. Subtract the smaller number (12) from the larger number (18): 18 - 12 = 6
- Step 3: We now have the numbers 12 and 6. Subtract the smaller number (6) from the larger number (12): 12 - 6 = 6
- Step 4: We have 6 and 6. Since the numbers are the same, the GCF is 6.
The Euclidean algorithm provides a concise and efficient way to find the GCF, even for very large numbers. It's a cornerstone algorithm in number theory and computer science.
Beyond the Basics: Exploring GCF Concepts
Understanding the GCF of 18 and 30 is just the beginning. Let's delve deeper into related concepts:
Least Common Multiple (LCM)
The least common multiple (LCM) is the smallest positive integer that is a multiple of both numbers. The GCF and LCM are related by the following formula:
GCF(a, b) x LCM(a, b) = a x b
Using this formula, we can find the LCM of 18 and 30:
GCF(18, 30) = 6
6 x LCM(18, 30) = 18 x 30
LCM(18, 30) = (18 x 30) / 6 = 90
Therefore, the LCM of 18 and 30 is 90.
Applications in Fraction Simplification
The GCF is instrumental in simplifying fractions. Consider the fraction 18/30. By dividing both the numerator (18) and the denominator (30) by their GCF (6), we simplify the fraction:
18/30 = (18 ÷ 6) / (30 ÷ 6) = 3/5
The simplified fraction 3/5 represents the same value as 18/30 but is in its simplest form.
GCF in Geometry
Consider a rectangular garden with dimensions 18 meters by 30 meters. If you want to divide the garden into identical square plots, the largest possible square plot would have sides equal to the GCF of 18 and 30, which is 6 meters. You could fit 3 plots along the 18-meter side and 5 plots along the 30-meter side, creating 15 identical square plots.
GCF in Real-World Problem Solving
Imagine you have 18 apples and 30 oranges. You want to create gift bags with an equal number of apples and oranges in each bag. The maximum number of gift bags you can create is determined by the GCF of 18 and 30, which is 6. Each bag would contain 3 apples and 5 oranges.
Conclusion: Mastering GCF Calculations
This in-depth exploration of finding the GCF for 18 and 30 has not only provided the answer (6) but also equipped you with multiple methods for calculating GCFs, including listing factors, prime factorization, and the Euclidean algorithm. By understanding these methods and their applications, you'll be better prepared to tackle more complex mathematical problems and appreciate the practical value of GCFs across various fields. Remember that choosing the most efficient method depends on the numbers involved – for smaller numbers, listing factors might suffice, while prime factorization and the Euclidean algorithm are better suited for larger numbers. The key is understanding the underlying principles, allowing you to apply these concepts with confidence and efficiency. Mastering GCF calculations is a crucial step towards developing a strong foundation in mathematics and problem-solving.
Latest Posts
Latest Posts
-
Is A Business Bachelor A Bachelor Of Art
Apr 08, 2025
-
How Many Oz In A Bottle Of Tequila
Apr 08, 2025
-
How Many Feet In 3 4 Acre
Apr 08, 2025
-
How Much Does A Bag Of Sugar Weigh
Apr 08, 2025
-
How Long Is 182 Days In Months
Apr 08, 2025
Related Post
Thank you for visiting our website which covers about What Is The Gcf For 18 And 30 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.